Определение. Квадратным уравнением (или уравнением второй степени) называется уравнение вида  , где
, где  - заданные числа, причем
- заданные числа, причем 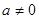 , а
, а  - неизвестное. Числа
- неизвестное. Числа  называются коэффициентами квадратного уравнения:
называются коэффициентами квадратного уравнения:  - коэффициент при квадрате неизвестного,
- коэффициент при квадрате неизвестного,  - коэффициент при неизвестном в первой степени,
- коэффициент при неизвестном в первой степени,  - свободный член.
- свободный член.
Квадратное уравнение  называется неполным, если хотя бы один из коэффициентов
называется неполным, если хотя бы один из коэффициентов  или
или  равен нулю.
равен нулю.
Неполное квадратное уравнение - это уравнение одного из следующих видов:



Покажем, как решаются неполные квадратные уравнения.
1. Уравнение  имеет единственный корень
имеет единственный корень  .
.
2. Уравнение  равносильно уравнению
равносильно уравнению  . Возможны два случая.
. Возможны два случая.
Если  , то
, то  , и поэтому уравнение
, и поэтому уравнение  не имеет действительных корней.
не имеет действительных корней.
Если  , то
, то  , и уравнение
, и уравнение  имеет два корня:
имеет два корня:  ,
, 
 .
.
Действительно, перенося в уравнении  величину
величину  в левую часть, получаем
в левую часть, получаем  .
.
Так как  , то
, то  . Поэтому
. Поэтому  .
.
Разложив левую часть этого уравнения на множители, получим  .
.
Данное произведение равно нулю, если хотя бы один из сомножителей равен нулю.
Рассматривая  , получим
, получим  ; рассматривая
; рассматривая  , находим
, находим  .
.
Следовательно, уравнение  при
при  имеет два корня;
имеет два корня;  ,
,  что и утверждалось. Ответ часто записывается в виде
что и утверждалось. Ответ часто записывается в виде  .
.
Например, неполное квадратное уравнение  не имеет действительных корней. Для неполного квадратного уравнения
не имеет действительных корней. Для неполного квадратного уравнения  получаем
получаем 
Это уравнение можно решить по-другому:

3. Уравнение  можно решить с помощью разложения его левой части на множители. Очевидно, что
можно решить с помощью разложения его левой части на множители. Очевидно, что  , откуда
, откуда  ,
,  . Например,
. Например,  , откуда
, откуда  ,
,  .
.
В общем случае для решения квадратных уравнений применяется метод выделения полного квадрата. [5, c.120]
Применение этого метода поясним сначала на примерах.
Пример 1. Решить квадратное уравнение 
Решение. Разделим обе части уравнения на  :
:
 .
.
Применим метод выделения полного квадрата:  .
.
Поэтому получим
 ,
,
откуда  . Следовательно,
. Следовательно,
 ,
,  .
.
Можно выделить полный квадрат в исходном уравнении и без предварительного деления на  (коэффициент при квадрате неизвестного):
(коэффициент при квадрате неизвестного):
 .
.
Поэтому
 и т.д. [2, c.107]
и т.д. [2, c.107]
Рассмотрим теперь квадратное уравнение общего вида

 . (1)
. (1)
Применим метод выделения полного квадрата. Для этого запишем левую часть уравнения в следующем виде:
 .Поэтому
.Поэтому
 или
или  . (2)
. (2)
Дальнейшее решение зависит от знака правой части полученного уравнения (2).
Так как  , то знак правой части совпадает со знаком выражения
, то знак правой части совпадает со знаком выражения  . [15, c.163]
. [15, c.163]
Определение. Выражение  называется дискриминантом квадратного уравнения
называется дискриминантом квадратного уравнения 
 и обозначается буквой
и обозначается буквой  :
:  .
.
Рассмотрим три случая:  .
.
1.  .
.
В этом случае уравнение (2) можно записать так:
 ;
;
следовательно,
 ,
,
откуда
 , (3)
, (3)
или
 , (4)
, (4)
где  - дискриминант уравнения (1).
- дискриминант уравнения (1).
Таким образом, в случае положительного дискриминанта, т.е. при  , уравнение
, уравнение  имеет два различных корня, которые можно найти по формуле (3) или (4).
имеет два различных корня, которые можно найти по формуле (3) или (4).
2.  .
.
В этом случае уравнение (2) принимает вид
 ,
,
откуда  , т.е.
, т.е.  .
.
Таким образом, если дискриминант равен нулю, т.е.  , то уравнение имеет единственный корень
, то уравнение имеет единственный корень  .
.
Заметим, что формула (3) или, что то же, (4) применима и в случае  . В самом деле, эта формула дает единственный корень уравнения (1). Говорят также, что в этом случае квадратное уравнение имеет два равных корня:
. В самом деле, эта формула дает единственный корень уравнения (1). Говорят также, что в этом случае квадратное уравнение имеет два равных корня:  . Такое соглашение освобождает нас от специальных оговорок, относящихся к этому случаю при формулировке свойств квадратных уравнений.
. Такое соглашение освобождает нас от специальных оговорок, относящихся к этому случаю при формулировке свойств квадратных уравнений.
3.  .
.
В этом случае в правой части уравнения (2) стоит отрицательное число, а в левой части - неотрицательное (положительное или равное нулю). Следовательно, если  , то уравнение (2), а значит, и уравнение
, то уравнение (2), а значит, и уравнение  не имеют действительных корней.
не имеют действительных корней.
Вывод. Квадратное уравнение  имеет действительные корни только при дискриминанте
имеет действительные корни только при дискриминанте  ; если
; если  , то корни различные; если
, то корни различные; если  , то корни равные. Формула корней квадратного уравнения имеет вид (3) или (4). [15, c.165]
, то корни равные. Формула корней квадратного уравнения имеет вид (3) или (4). [15, c.165]
По этой формуле можно находить и корни неполных квадратных уравнений, но проще вычислять их путем разложения левой части неполного квадратного уравнения на множители, как было показано.
Замечание 1. Если коэффициент  - четное число, т.е.
- четное число, т.е.  , то формула корней квадратного уравнения примет вид
, то формула корней квадратного уравнения примет вид
 . [2, c.114]
. [2, c.114]
Например, вычислим корни уравнения  (заметим, что уравнение имеет действительные корни, так как
(заметим, что уравнение имеет действительные корни, так как  ):
):
 .
.
Замечание 2. Если коэффициент  , то квадратное уравнение принимает вид
, то квадратное уравнение принимает вид  . Такое квадратное уравнение называется приведенным квадратным уравнением. Всякое квадратное уравнение
. Такое квадратное уравнение называется приведенным квадратным уравнением. Всякое квадратное уравнение  можно привести к виду
можно привести к виду  делением обеих частей уравнения на
делением обеих частей уравнения на  . [2, c.117]
. [2, c.117]
Найдем корни приведенного квадратного уравнения. В формуле (3) полагаема  . Тогда
. Тогда
 - формула корней приведенного квадратного уравнения
- формула корней приведенного квадратного уравнения  .
.
Например, решим уравнение  :
:
 ,
,
Откуда 
Пример 2. Решить уравнение  .
.
Решение. Разложив знаменатели на множители, имеем
 .
.
После приведения дробей к общему знаменателю  получим уравнение
получим уравнение  или
или  , равносильное исходному уравнению, при условии, что
, равносильное исходному уравнению, при условии, что  , т.е.
, т.е.  ,
,  . Находим корни приведенного квадратного уравнения:
. Находим корни приведенного квадратного уравнения:
 ,
,
откуда  ,
,  . Так как
. Так как  не удовлетворяет ограничению
не удовлетворяет ограничению  (не входит в ОДЗ исходного уравнения), то, следовательно, исходное уравнение имеет единственный корень
(не входит в ОДЗ исходного уравнения), то, следовательно, исходное уравнение имеет единственный корень  . [2, c.124]
. [2, c.124]
Теорема Виета. Если квадратное уравнение  имеет действительные корни
имеет действительные корни  и
и  , то их сумма равна
, то их сумма равна  и произведение равно
и произведение равно  :
:
 ,
,  . (5)
. (5)
Формулы (5) называются формулами Виета.
Доказательство. По условию дискриминант квадратного уравнения  . Тогда по формуле (4) уравнение имеет два корня:
. Тогда по формуле (4) уравнение имеет два корня:
 ,
,  .
.
Найдем сумму и произведение корней:
 ,
,
 ,
,
и формулы (5) получены.
Теорема Виета устанавливает связь между корнями квадратного уравнения и его коэффициентами.
Для приведенного квадратного уравнения  с дискриминантом
с дискриминантом  формулы (5) принимают вид
формулы (5) принимают вид
 ,
,  . (6)
. (6)
Полученные для приведенного квадратного уравнения формулы Виета читаются так: сумма корней приведенного квадратного уравнения равна коэффициенту при неизвестном в первой степени, взятому с противоположным знаком, а произведение корней равно свободному члену.
Если корни квадратного уравнения действительные  , то формулы Виета позволяют по знакам коэффициентов уравнения определить знаки корней. Например, если
, то формулы Виета позволяют по знакам коэффициентов уравнения определить знаки корней. Например, если  ,
,  ,
,  (и, следовательно,
(и, следовательно,  ), то
), то  и корни имеют разные знаки. Так как при этом
и корни имеют разные знаки. Так как при этом  , то отсюда следует, что больший по модулю корень отрицателен (сумма двух чисел разных знаков отрицательная!). [5, c.126]
, то отсюда следует, что больший по модулю корень отрицателен (сумма двух чисел разных знаков отрицательная!). [5, c.126]
Теорема (обратная теореме Виета). Если числа  таковы, что
таковы, что  ,
,  , то
, то  и
и  - корни уравнения
- корни уравнения  .
.
В теореме Виета для приведенного квадратного уравнения  утверждалось, что для его корней
утверждалось, что для его корней  ,
,  и коэффициентов
и коэффициентов  справедливы формулы (6).
справедливы формулы (6).
В обратной теореме Виета утверждается: если для чисел  справедливы формулы (6), то
справедливы формулы (6), то  и
и  - корни приведенного квадратного уравнения
- корни приведенного квадратного уравнения  .
.
Доказательство. Рассмотрим  и получим
и получим  . Очевидно, что
. Очевидно, что  и
и  - корни уравнения
- корни уравнения  и, значит, уравнения
и, значит, уравнения  . [5, c.127]
. [5, c.127]
Теорема Виета и теорема, обратная ей, часто применяются при решении различных задач.
Пример 3. Не решая уравнения  , определить знаки его корней.
, определить знаки его корней.
Решение. Дискриминант этого уравнения положителен, так как  . Следовательно, уравнение имеет действительные корни
. Следовательно, уравнение имеет действительные корни  и
и  . По теореме Виета
. По теореме Виета  ; корни имеют одинаковые знаки. Так как по теореме Виста
; корни имеют одинаковые знаки. Так как по теореме Виста  , то корни
, то корни  и
и  - положительные. [2, c.119]
- положительные. [2, c.119]
Пример 4. Составить приведенное квадратное уравнение, корни которого  ,
, 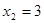 .
.
Решение. По обратной теореме Виета  ,
,  . Искомое уравнение
. Искомое уравнение  . [2, c.119]
. [2, c.119]
 2020-01-14
2020-01-14 238
238








