Краевые задачи электростатики проводников

      11.1. Постановка краевых задач. Электростатическое поле в вакууме (воздухе) удовлетворяет уравнениям

 .

Если ввести электрический потенциал, уравнения принимают вид:

 .

Подставим первое уравнение во второе:

 .

(уравнение Пуассона). Если в пространстве между заряженными проводниками нет заряженных тел ( =0), то электрический потенциал подчиняется уравнению Лапласса

.

     Потенциалы проводников являются постоянными величинами, их значения составляют естественные граничные (краевые) условия. Поверхности проводников являются границами области, в которой существует электрическое поле. Внутри проводников электрического поля нет. Если поле распространяется в трехмерном пространстве до бесконечности, роль граничного условия приобретает выбор точки нулевого потенциала на бесконечности,

     В двумерных задачах точку нулевого потенциала можно выбрать на бесконечности, если система уравновешена, т.е. сумма положитель ных и отрицательных зарядов в рассматриваемой системе равна нулю.

    Если по условию задачи заданы не потенциалы, а заряды проводников, то решение несколько усложняется. Задавая разные комбинации потенциалов проводников (в числах) и определяя соответствующие этим потенциалам заряды (после расчета поля), можно найти потенциальные коэффициенты проводников. После этого нетрудно найти потенциалы, соответствующие любым зарядам проводиков.

11.2. Примеры. 1. Электрическое поле уединённого заряженного проводника. В пространстве вокруг проводника электрический потенциал удовлетворяет уравнению Лапласа  . Граничные условия: на поверхности проводника  (известная постоянная), на бесконечности . Эта краевая задача получила название внешней задачи Дирихле.

      Примечание. Для проводников простой формы (шар, круговой диск) задача решается аналитически. Поле проводников сложной формы рассчитывается приближёнными численными методами. Дифференциальный оператор в уравнении Лапласа заменяется конечно-разностным выражением, а условие приближенным условием

на сфере достаточно большого радиуса R, в середине которой находится рассматриваемый проводник с зарядом q. Заряд этот не известен, но связан с искомым потенциалом условием

Следовательно,

Для множества узловых точек на поверхности проводника и вокруг него вплоть до сферы радиуса R с помощью уравнения Лапласа в конечно-разностной форме и граничных условий получается система линейных алгебраических уравнений относительно искомых значений потенциала.

    Если задан не потенциал, а заряд проводника q, то можно решить краевую задачу с граничным условием  и затем найти соответствующий этому условию заряд  по формуле(21). Потенциальный коэффициент проводника

,

потенциал проводника с зарядом q равен

.

        Примечание. Решать краевую задачу с новым граничным условием  ненужно. Найденные в предварительном расчете значения потенциала в узловых точках нужно умножить на q (как и значение потенциала на поверхности проводника).

2.Электрическое поле экранированного шинопровода.

Шинопровод- это линия передачи электрической энергии на небольшие расстояния при больших токах и сравнительно небольших напряжениях. Обычно он состоит из двух или трех проводов (шин) с большим поперечным сечением, изолированных друг от друга большим воздушным промежутком. Шинопровод помещают в длинную металлическую коробку (экран), которая, во-первых, защищает шины от внешнего механического воздействия, во-вторых, не позволяет распространяться электрическому полю шин за пределы экрана. На рис.21 показано поперечное шинопровода с двумя шинами.

Рис.21. Поперечное сечение системы длинных проводников.

        Электрическое поле шинопровода является двумерным,       .Потенциал в воздухе внутри экрана вокруг шин удовлетворяет уравнению Лапласа

Экран обычно заземляется, его потенциал .Шины присоединены к зажимам источника электрической энергии, на них поступают равные по величине и противоположные по знаку заряды, напряжение между шинами равно напряжению источника u. Можно принять, что потенциал первой шины равен , потенциал второй . Таким образом, на границах трехсвязной области в плоскости XOY, ограниченной тремя замкнутыми линиями (рис.21), заданы потенциалы. Эта краевая задача в математической физике называется внутренней задачей Дирехле.

      В рассмотренной задаче заряды проводников подчиняются условиям        . Система проводников полностью характеризуется ёмкостью между шинами . В общем случае, когда заряды проводников различны               (), система характеризуется девятью потенциальными коэффициентами ,где i и k принимают значения 0,1,2. Можно показать, что взаимные потенциальные коэффициенты одинаковы, т.е.  Практически потенциальных коэффициентов в системе не 9, а 6.

     11.3 Дополнения к §11. Заряженный проводник во внешнем электрическом поле. Допустим для определённости, что проводник находится в поле точечного заряда (рис.18). В такого рода задачах потенциал проводника , как правило, не известен, а заданы его заряд  и точечный заряд . Тогда краевая задача сводится к двум краевым задачам, которые решаются одна за другой, а потом из их решений конструируется решение исходной задачи.

     Искомое поле создано точечным зарядом  и проводником с зарядом  и неизвестным потенциалом . Обозначим потенциал этого поля через φ.Обозначим потенциал этого поля через φ. В первой краевой задаче фигурирует поле потенциала φ, которое создаётся точечным зарядом  и проводником с зарядом  и известным потенциалом . Во второй краевой задаче определяется поле потенциала φ״, которое создается одним заряженным проводником с зарядом  и потенциалом , в условии задачи не заданным. Искомый потенциал складывается из решений первой и второй задачи  так, чтобы

на поверхности проводника. Постоянная  подбирается так, чтобы заряд проводника был равен величине , заданной в условии задачи.

     Итак, начнем с того, что потенциалу проводника

припишем некоторое значение φ. Здесь предполагается, что точка наблюдения 1 находится на поверхности проводника S. Интеграл представляет потенциал поля, созданным собственным зарядом проводника; обозначим его через ψ'. На поверхности проводника S

,

 

Эта функция легко вычисляется. В пространстве вокруг проводника его собственное поле удовлетворяет уравнению Лапласса . (как потенциал простого слоя) и подчиняется граничным условиям . и =  на поверхности проводника S. Для поля потенциала  получилась типичная внешняя задача Дирихле.

     Складывая поле  с полем точечного заряда 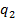, получаем решение первой краевой задачи

При этом на поверхности проводника = 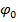. Определим заряд проводника, соответствующий его потенциалу :

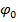Если окажется, что  равняется  (заданному по условию исходной задачи заряду проводника), то решение первой краевой задачи φ ׳ (x,y,z) является решением исходной задачи. Однако маловероятно, что сразу удастся угадать значение потенциала проводника, соответствующего его заряда .

     Перейдем к формулировке второй краевой задачи. Как было показано в дополнении к § 10, потенциал проводника линейно зависит от его собственнго заряда  и внешнего заряда :

Применительно к результатам решения первой краевой задачи получается, что

 

В этом уравнении содержится два неизвестных потенциальных коэффициента  и . Чтобы найти их, требуется еще одно соотношение между потенциалом проводника и зарядами. Можно еще решить первую краевую задачу при другом значении потенциала проводника, отличном от 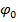. Однако рациональнее принять, что заряд проводника равен заданной величине , а точечный заряд отсутствует, т.е. =0. Постановка этой задачи аналогична краевой задаче, рассмотренной в п.11.2(пример 1). Это и есть вторая краевая задача.

     Решение второй краевой задачи дает поле потенциала φ ״ (x,y,z), при этом потенциал проводника принимает значение , соответствующее заряду . Потенциальный коэффициент . Теперь из равенства(23) можно найти , а затем потенциал проводника в исходной задаче по формуле (22).

     Остается сконструировать решение сформулированной в начале задачи из решений первой и второй краевых задач. Как отмечалось выше, потенциал проводника 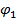 в поле точечного заряда  складывается из значения = ,выбранного в первой краевой задаче, и величины k , пропорциональной потенциалу , полученному при решении второй краевой задачи: = 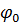+ . Отсюда находим неизвестный коэффициент

     Здесь потенциалы выражены через заряды с помощью формул (22) и (23), а -заряд проводника при условии, что его потенциал равен 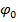. Обычно при решении первой краевой задачи полагают, что =0.

     Таким образом, чтобы рассчитать электрическое поле заряженного проводника, находящемся во внешнем поле, при условии, что задан потенциал проводника 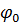, нужно решить первую краевую задачу. Если задан заряд проводника , то сначала нужно решить первую краевую задачу при некотором значении потенциала проводника 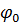 и найти его заряд  при таком потенциале. Затем нужно решить вторую краевую задачу для уединенного проводника с зарядом . Наконец, поле проводника зарядом  при наличии внешнего поля получается объединением решений двух краевых задач

.