
Задание 2.
Вычислите определитель

Задание 3.
Решите систему уравнений по формулам Крамера и проверьте решение подстановкой

Вариант 14.
Задание 1.
Найдите значение матричного выражения

Задание 2.
Вычислите определитель

Задание 3.
Решите систему уравнений по формулам Крамера и проверьте решение подстановкой

Вариант 15.
Задание 1.
Найдите значение матричного выражения
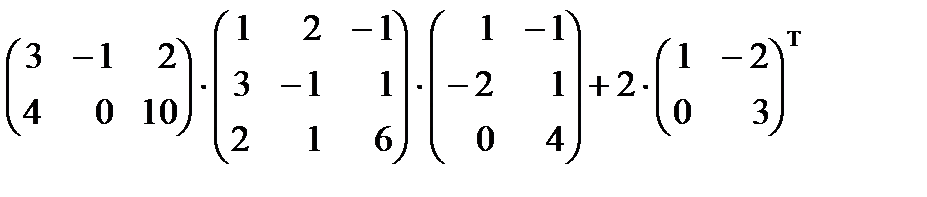
Задание 2.
Вычислите определитель

Задание 3.
Решите систему уравнений по формулам Крамера и проверьте решение подстановкой

Составить 10 вопросов по данной теме.
Требования к оформлению лабораторной работы
Расчетные задания должны быть выполнены в электронном виде на сайтах http://ru.onlinemschool.com/math/assistance/vector/pyramid_volume/
http://matematikam.ru/calculate-online/grafik.php
https://www.kontrolnaya-rabota.ru/s/grafik/polyar
Лабораторная работа №3.
Наименование: «Элементы векторной алгебры и аналитической геометрии»
Цель работы: развитие умений и навыков по выполнению действий над векторами, составлению уравнений линий.
|
|
|
Основной теоретический материал
Кривые второго порядка.
Основные понятия
Линии, определяемые уравнениями второй степени относительно текущих координат
(1) Ax2+2By+Cy2+2Dx+2Ey+F=0, где коэффициент уравнения- действительная числа, по крайней мере одно из чисел a,b или с отличны от 0, называются линиями (кривыми) второго порядка.
Уравнение (1) определяет на плоскости окружность, эллипс, гиперболу или параболу.
Окружность.
Окружностью называется множество всех точек плоскости равноудаленных от данной точки этой плоскости, называемой центром.
Уравнение окружности с центром в начале координат и радиусом r имеет вид x2+y2=r2.
Уравнение окружности в общем виде записывается так Ax2+Аy2+Вх+Cy+D =0, где А, В,С и D- постоянные коэффициенты
Эллипс.
Эллипсом называется множество точек плоскости сумма расстояния которых до двух данных точек, называемых фокусами, есть величина постоянная (2а) большая расстояния между фокусами (2с).
Уравнение эллипса, фокусы которых лежит на оси Ох, имеет вид


b- длина малой полуоси
Зависимость между параметрами a, b и c выражается соотношением a2- b2 = c2
Эксцентриситетом эллипса называется отношение фокусного расстояния 2с к большей оси 2а:

Если фокусы эллипса лежат на оси Оу, то его уравнение имеет вид:


Гипербола.
Гиперболой называется множество точек плоскости, абсолютная величина разности расстояния которого до двух данных точек, называется фокусами, есть величина постоянная (2а),меньшая расстояние между фокусами (2с).
Уравнение гиперболы,фокусы которого лежит на оси Ох, имеет вид:  где а- длина действительной полуоси
где а- длина действительной полуоси
|
|
|
b- длина малой полуоси
Зависимость между параметрами a,b и c выпажается соотношением: b2 = c2 - a2 (2)
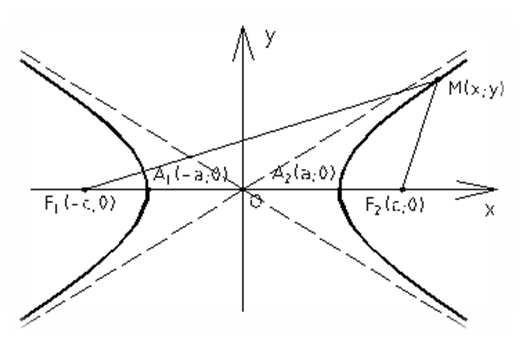
Эксцентриситетом гиперболы называется отношение фокусного расстояния к ее действительной оси:

Гипербола имеет две асимптоты, уравнения которых:

Если действительная и мнимая оси гиперболы равны (т.е. a=b), то гипербола называется равносторонним. Уравнение гипреболы записывается в виде:
х2-у2=а2, а- уравнение ее асимптот

Если фокусы гиперболы лежат на оси Оу, то ее уравнение имеет вид:
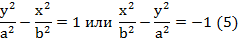
Уравнения асимптот такой гиперболы

Формулы (2) и (3) для гиперболы с фокусами на оси Оу остаются без изменений. Гиперболы (1) и (5) называются спряженными.
Уравнение равносторонней гиперболы с фокусами на оси Он имеет вид у2-х2=а2
Во всех задачах на гиперболе предполагает что оси симметрии гиперболы совпадает с осями координат.
Парабола.
Параболой называется множество точек на плоскости, равноудаленных от данной точки, называемой фокусом, и от данной прямой, называемой директрисой.
Уравнение параболы с вершиной в начале координат, осью симметрии которой служит ось Ох и ветви направлении вправо имеет вид у2=2px, где p>0 (параметр параболы)-расстояние от фокуса до директрисы 
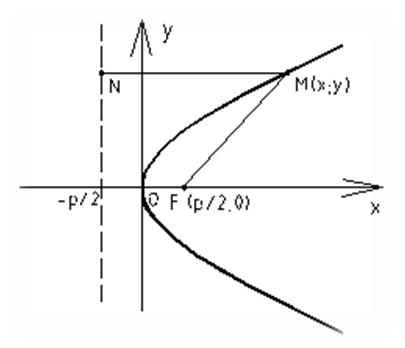
Уравнение параболы с вершиной в начале координат осью симметрии которого служит ось Ох и ветви направлены влево имеет вид:
Уравнение параболы с вершиной в начале координат, осью симметрии которого служит ось Оу и ветви направлены вниз, имеет вид х2 = -2py (p>0)
Уравнение ее директрисы y = 
Во всех задачах предполагается, что осью симметрии служит одна из осей координат.
Задание 1. Даны три вектора  . Найти координаты вектора
. Найти координаты вектора  :
:
1.  . 2.
. 2.  .
.
3.  . 4.
. 4.  .
.
5. 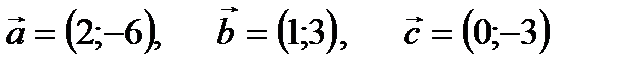 . 6.
. 6.  .
.
7.  . 8.
. 8.  .
.
9. 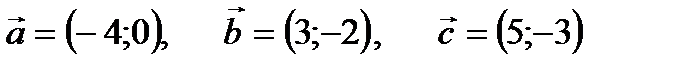 . 10.
. 10.  .
.
11.  . 12.
. 12.  .
.
13.  . 14.
. 14.  .
.
15.  . 16.
. 16.  .
.
17.  . 18.
. 18.  .
.
19.  . 20.
. 20.  .
.
21.  . 22.
. 22.  .
.
23.  . 24.
. 24.  .
.
25.  . 26.
. 26. 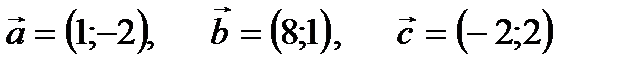 .
.
27.  . 28.
. 28.  .
.
29.  . 30.
. 30.  .
.
Задание 2. Даны координаты вершин пирамиды  . Найти: 1) длину ребра
. Найти: 1) длину ребра  ; 2) угол между рёбрами
; 2) угол между рёбрами  и
и  ; 3) площадь грани
; 3) площадь грани  ; 4) объём пирамиды; 5) уравнение прямой
; 4) объём пирамиды; 5) уравнение прямой  ; 6) уравнение плоскости
; 6) уравнение плоскости  . Сделать чертёж.
. Сделать чертёж.



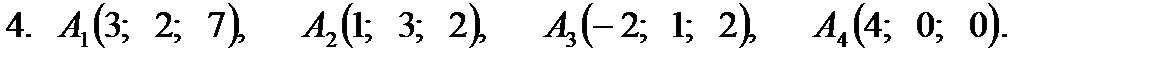

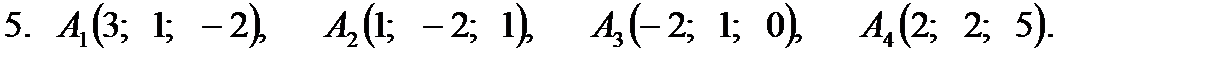




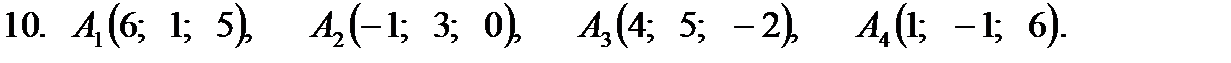




















Задание 3.
1. Показать, что данное уравнение  определяет окружность. Найти координаты её центра и радиус. Построить окружность.
определяет окружность. Найти координаты её центра и радиус. Построить окружность.
2. Найти каноническое уравнение эллипса, зная, что:  . Найти координаты фокусов эллипса. Построить эллипс.
. Найти координаты фокусов эллипса. Построить эллипс.
3. Составить уравнение гиперболы и построить её, если известны:  . Найти координаты фокусов гиперболы, эксцентриситет и уравнения асимптот.
. Найти координаты фокусов гиперболы, эксцентриситет и уравнения асимптот.
4. Дана парабола  . Найти уравнение её директрисы, координаты фокуса. Построить параболу.
. Найти уравнение её директрисы, координаты фокуса. Построить параболу.
5. Показать, что данное уравнение  определяет окружность. Найти координаты её центра и радиус. Построить окружность.
определяет окружность. Найти координаты её центра и радиус. Построить окружность.
6. Найти каноническое уравнение эллипса, зная, что:  . Найти координаты фокусов эллипса. Построить эллипс.
. Найти координаты фокусов эллипса. Построить эллипс.
7. Дано уравнение гиперболы  . Найти координаты фокусов гиперболы, эксцентриситет и уравнения асимптот. Построить гиперболу.
. Найти координаты фокусов гиперболы, эксцентриситет и уравнения асимптот. Построить гиперболу.
8. Дана парабола  . Найти уравнение её директрисы, координаты фокуса. Построить параболу.
. Найти уравнение её директрисы, координаты фокуса. Построить параболу.
9. Показать, что данное уравнение  определяет окружность. Найти координаты её центра и радиус. Построить окружность.
определяет окружность. Найти координаты её центра и радиус. Построить окружность.
10. Найти каноническое уравнение эллипса, зная, что:  . Найти координаты фокусов эллипса. Построить эллипс.
. Найти координаты фокусов эллипса. Построить эллипс.
11. Дано уравнение гиперболы  . Найти координаты фокусов гиперболы, эксцентриситет и уравнения асимптот. Построить гиперболу.
. Найти координаты фокусов гиперболы, эксцентриситет и уравнения асимптот. Построить гиперболу.
12. Дана парабола  . Найти уравнение её директрисы, координаты фокуса. Построить параболу.
. Найти уравнение её директрисы, координаты фокуса. Построить параболу.
13. Показать, что данное уравнение 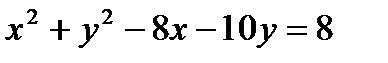 определяет окружность. Найти координаты её центра и радиус. Построить окружность.
определяет окружность. Найти координаты её центра и радиус. Построить окружность.
|
|
|
14. Найти каноническое уравнение эллипса, зная, что:  . Найти координаты фокусов эллипса. Построить эллипс.
. Найти координаты фокусов эллипса. Построить эллипс.
15. Составить уравнение гиперболы и построить её, если известны координаты фокусов гиперболы  и эксцентриситет равен 2.
и эксцентриситет равен 2.
16. Дана парабола  . Найти уравнение её директрисы, координаты фокуса. Построить параболу.
. Найти уравнение её директрисы, координаты фокуса. Построить параболу.
17. Показать, что данное уравнение 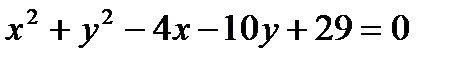 определяет окружность. Найти координаты её центра и радиус. Построить окружность.
определяет окружность. Найти координаты её центра и радиус. Построить окружность.
18. Найти каноническое уравнение эллипса, зная, что:  . Найти координаты фокусов эллипса. Построить эллипс.
. Найти координаты фокусов эллипса. Построить эллипс.
19. Составить уравнение гиперболы и построить её, если известны координаты фокусов гиперболы  и уравнения асимптот
и уравнения асимптот  .
.
20. Дана парабола  . Найти уравнение её директрисы, координаты фокуса. Построить параболу.
. Найти уравнение её директрисы, координаты фокуса. Построить параболу.
21. Показать, что данное уравнение  определяет окружность. Найти координаты её центра и радиус. Построить окружность.
определяет окружность. Найти координаты её центра и радиус. Построить окружность.
22. Найти каноническое уравнение эллипса, зная, что:  . Найти координаты фокусов эллипса. Построить эллипс.
. Найти координаты фокусов эллипса. Построить эллипс.
23. Дано уравнение гиперболы  . Найти координаты фокусов гиперболы, эксцентриситет и уравнения асимптот. Построить гиперболу.
. Найти координаты фокусов гиперболы, эксцентриситет и уравнения асимптот. Построить гиперболу.
24. Дана парабола  . Найти уравнение её директрисы, координаты фокуса. Построить параболу.
. Найти уравнение её директрисы, координаты фокуса. Построить параболу.
25. Показать, что данное уравнение  определяет окружность. Найти координаты её центра и радиус. Построить окружность.
определяет окружность. Найти координаты её центра и радиус. Построить окружность.
26. Найти каноническое уравнение эллипса, зная, что:  . Найти координаты фокусов эллипса. Построить эллипс.
. Найти координаты фокусов эллипса. Построить эллипс.
27. Составить каноническое уравнение гиперболы и построить её, если известно, что:  . Найти координаты фокусов гиперболы и уравнения асимптот.
. Найти координаты фокусов гиперболы и уравнения асимптот.
28. Дана парабола  . Найти уравнение её директрисы, координаты фокуса. Построить параболу.
. Найти уравнение её директрисы, координаты фокуса. Построить параболу.
29. Показать, что данное уравнение  определяет окружность. Найти координаты её центра и радиус. Построить окружность.
определяет окружность. Найти координаты её центра и радиус. Построить окружность.
30. Найти каноническое уравнение эллипса, зная, что:  . Найти координаты фокусов эллипса. Построить эллипс.
. Найти координаты фокусов эллипса. Построить эллипс.
Задание 4. Дана функция  . Требуется построить линию по точкам, начиная от
. Требуется построить линию по точкам, начиная от  до
до  , придавая
, придавая  значения через промежуток
значения через промежуток 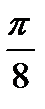 .
.








|
|
|














 .
. 


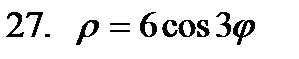 .
. 
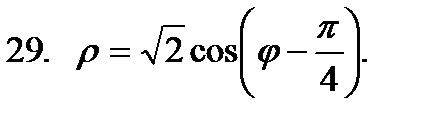
 .
.
 2020-05-11
2020-05-11 191
191








