а) Уравнения вида  .
.
Общее решение такого уравнения получим, производя последовательно два интегрирования:
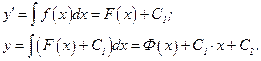
б) Уравнения, не содержащие явно неизвестную функцию:  .
.
Это уравнение можно свести к уравнению первого порядка, если за новую неизвестную функцию взять производную  :
:  ,
,  . В результате получим:
. В результате получим:  .
.
в) Уравнения, не содержащие явно независимую переменную: 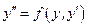 .
.
Порядок такого уравнения понижается путем замены обеих переменных. За новую переменную выберем 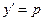 , а за новую независимую переменную принимаем
, а за новую независимую переменную принимаем  . Тогда имеем:
. Тогда имеем:  ,
,  . Данное уравнение принимает вид:
. Данное уравнение принимает вид:  .
.
○ Пример 1. Найти общее решение дифференциального уравнения второго порядка 
Решение.


Пример 2. Найти общее решение дифференциального уравнения второго порядка  .
.
Решение. Это уравнение не содержит явным образом неизвестную функцию  .
.
 ,
,  .
.
Получим:  – линейное уравнение относите6льно функции
– линейное уравнение относите6льно функции 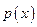 .
.
Пусть  . Тогда,
. Тогда,


1) 

2) 

3) 

Мы обозначили  . Таким образом,
. Таким образом,

Пример 3. Найти общее решение дифференциального уравнения второго порядка  .
.
|
|
|
Решение. В это уравнение не входит  . Положим
. Положим  , тогда
, тогда 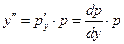 . Подставляя в данное уравнение, получим:
. Подставляя в данное уравнение, получим:
 .
.
Это уравнение с разделяющимися переменными.

Следовательно,






Из этого уравнения выразим неизвестную функцию:

Задача типа 6.
Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.
1. Линейное однородное (без правой части) уравнение второго порядка с постоянными коэффициентами  и
и  имеет вид
имеет вид
 . (1)
. (1)
Для отыскания общего решения составляют характеристическое уравнение
 .
.
В зависимости от корней  и
и  этого уравнения общее решение дифференциального уравнения (1) записывают в виде
этого уравнения общее решение дифференциального уравнения (1) записывают в виде
1) 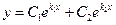 ,
,
если  и
и  действительные и
действительные и  .
.
2)  ,
,
если  и
и  действительные и
действительные и  .
.
3)  ,
,
если  и
и  - пара сопряженных комплексных чисел,
- пара сопряженных комплексных чисел, 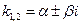 .
.
○ Пример. Найти общее решение уравнения
а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 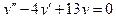 ; д)
; д)  .
.
Решение. а) 
Составим характеристическое уравнение 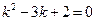 .
.
Корни этого уравнения 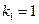 и
и  - действительные и различные. Общее решение данного уравнения запишем в виде
- действительные и различные. Общее решение данного уравнения запишем в виде
 .
.
б)  ;
;  ;
;  ;
;  и
и 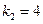 ;
;  .
.
в)  ;
; 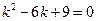 ;
;  ;
;  .
.
г)  ;
;  ;
;  ;
;  и
и  ;
;  .
.
д)  ;
;  ;
;  ;
;  ;
;  и
и  ;
;  .
.
2. Линейное неоднородное уравнение второго порядка с постоянными коэффициентами имеет вид
|
|
|
 .
.
Его общее решение можно записать в виде суммы
 ,
,
где  - общее решение соответствующего однородного уравнения (1),
- общее решение соответствующего однородного уравнения (1),  - частное решение данного уравнения.
- частное решение данного уравнения.
Функция  может быть найдена методом неопределенных коэффициентов в следующих простейших случаях
может быть найдена методом неопределенных коэффициентов в следующих простейших случаях
1) Пусть  , тогда
, тогда
а)  , если число
, если число  не является корнем характеристического уравнения;
не является корнем характеристического уравнения;
б) 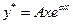 , если число
, если число  является корнем характеристического уравнения;
является корнем характеристического уравнения;
в)  , если число
, если число  является двукратным корнем характеристического уравнения.
является двукратным корнем характеристического уравнения.
2) Пусть 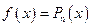 , где
, где  - многочлен степени
- многочлен степени  , тогда
, тогда
а)  , если нуль не является корнем характеристического уравнения;
, если нуль не является корнем характеристического уравнения;
б)  , если нуль является корнем характеристического уравнения.
, если нуль является корнем характеристического уравнения.
 - многочлен с неопределенными коэффициентами степени
- многочлен с неопределенными коэффициентами степени  .
.
Например,  , тогда
, тогда 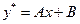 ;
;
 , тогда
, тогда 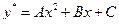 .
.
3) Пусть  , тогда
, тогда
а)  , если
, если  не является корнем характеристического уравнения;
не является корнем характеристического уравнения;
б)  , если
, если  является корнем характеристического уравнения.
является корнем характеристического уравнения.
○ Пример 1. Найти общее решение уравнения  .
.
Решение. Характеристическое уравнение  имеет корни
имеет корни  и
и  . Общее решение соответствующего однородно уравнения
. Общее решение соответствующего однородно уравнения 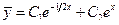 .
.
Правая часть этого уравнения 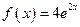 (случай 1). Число
(случай 1). Число  не является корнем характеристического уравнения. Поэтому
не является корнем характеристического уравнения. Поэтому  . Подберем коэффициент
. Подберем коэффициент  так, чтобы функция
так, чтобы функция  была решением данного дифференциального уравнения. Для этого найдем производные первого и второго порядков функции
была решением данного дифференциального уравнения. Для этого найдем производные первого и второго порядков функции  и подставим в данное уравнение
и подставим в данное уравнение
 ;
; 


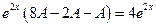

 .
.
Таким образом  .
.
Общее решение данного уравнения 
 .
.
○ Пример 2. Найти общее решение уравнения  .
.
Решение. Характеристическое уравнение  имеет два корня
имеет два корня  и
и 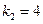 . Поэтому
. Поэтому  .
.
Правая часть уравнения  - многочлен первой степени (случай 2). Нуль является корнем характеристического уравнения. Поэтому
- многочлен первой степени (случай 2). Нуль является корнем характеристического уравнения. Поэтому 
Дифференцируя это выражение дважды и подставляя в данное уравнение получим
 ;
; 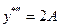

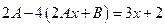
 .
.
Приравниваем коэффициенты при одинаковых степенях 
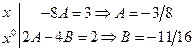 . Отсюда
. Отсюда  .
.
Общее решение данного уравнения
 .
.
○ Пример 3. Найти частное решение уравнения  , удовлетворяющее условиям
, удовлетворяющее условиям  при
при  .
.
Решение.
1)  ;
;  ;
;  ;
;  ;
;  .
.
2)  (4 случай).
(4 случай).

 ;
;  .
.
Подставим эти выражения в данное уравнение и приравняем коэффициенты при  и
и 


 . Отсюда
. Отсюда  .
.
Общее решение  . (*)
. (*)
Найдем частное решение, удовлетворяющее заданным начальным условиям  при
при  .
.
Продифференцируем функцию  и подставим начальные условия в выражения (*) и (**)
и подставим начальные условия в выражения (*) и (**)
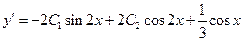 . (**)
. (**)
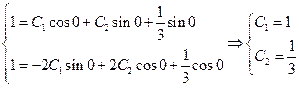 .
.
Искомое частное решение имеет вид
 .
.
Кратные интегралы
Пусть функция 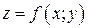 непрерывна в ограниченной замкнутой области
непрерывна в ограниченной замкнутой области  на плоскости
на плоскости  . Разобьем область
. Разобьем область  произвольным образом на
произвольным образом на  элементарных областей, имеющих площади
элементарных областей, имеющих площади  ,
,  , …,
, …,  , …,
, …,  . Выберем в каждой элементарной области точку
. Выберем в каждой элементарной области точку  и умножим значение функции в этой точке на площадь области
и умножим значение функции в этой точке на площадь области  . Двумерной интегральной суммой для функции
. Двумерной интегральной суммой для функции  по области
по области  называется сумма вида
называется сумма вида
 .
.
Двойным интегралом от функции  по области
по области  называется предел последовательности двумерных интегральных сумм, если он существует и не зависит от способа разбиения области
называется предел последовательности двумерных интегральных сумм, если он существует и не зависит от способа разбиения области  на части и выбора точек
на части и выбора точек  . Обозначается
. Обозначается


Если  в области
в области  , то двойной интеграл равен объему цилиндрического тела, ограниченного сверху поверхностью
, то двойной интеграл равен объему цилиндрического тела, ограниченного сверху поверхностью  , сбоку цилиндрической поверхностью с образующими, параллельными оси
, сбоку цилиндрической поверхностью с образующими, параллельными оси  , снизу областью
, снизу областью  плоскости
плоскости  . Площадь области
. Площадь области  равна
равна
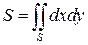 .
.
Свойства двойного интеграла аналогичны свойствам определенного интеграла. Вычисление двойного интеграла сводится к вычислению двукратного интеграла вида
1)  , если область
, если область  определена условиями:
определена условиями:  и
и 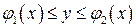 ;
;
 2)
2)  , если область
, если область  определена условиями:
определена условиями:  и
и  .
.
Переход от первого равенства ко второму или обратно называется изменением порядка интегрирования. Значение двойного интеграла не зависит от порядка интегрирования.
|
|
|
При вычислении двойного интеграла иногда бывает удобно перейти к полярным координатам
 .
.
Тройной интеграл от функции  по пространственной области
по пространственной области  определяется аналогично двойному интегралу
определяется аналогично двойному интегралу

Вычисление тройного интеграла сводится к вычислению трехкратного интеграла вида
 ,
,
где  - проекция области
- проекция области  на плоскость
на плоскость  ,
, 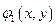 и
и  - уравнения поверхностей, ограничивающих область
- уравнения поверхностей, ограничивающих область  соответственно снизу и сверху.
соответственно снизу и сверху.
Объем тела можно вычислить по формуле
 .
.
Задача типа 7.
○ Пример 1. Изменить порядок интегрирования в двойном интеграле
 .
.
Решение. Зная пределы интегрирования, определим границы области интегрирования  .
.
Построим данную область
Определим точки пересечения данных линий

 .
.
Найдем новые пределы внутреннего (по  ) и внешнего (по
) и внешнего (по  ) интегралов. Слева область ограничена прямой
) интегралов. Слева область ограничена прямой  , откуда имеем
, откуда имеем 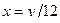 . Справа область ограничена параболой
. Справа область ограничена параболой 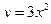 , откуда получим
, откуда получим  . Наименьшее значение
. Наименьшее значение  в заданной области равно 0, наибольшее 48. Итак, имеем
в заданной области равно 0, наибольшее 48. Итак, имеем
 .
.
○ Пример 2. Изменить порядок интегрирования в двойном интеграле

 .
.
Решение. Запишем уравнения линий, ограничивающих область, и построим ее
 .
.
Найдем новые пределы внутреннего (по  ) и внешнего (по
) и внешнего (по  ) интегралов. Область
) интегралов. Область  разобьем на две части
разобьем на две части  и
и  .
.
 .
.
Область  снизу и сверху ограничена ветвями параболы
снизу и сверху ограничена ветвями параболы  . Уравнения этих ветвей получим, выражая
. Уравнения этих ветвей получим, выражая  из уравнения параболы
из уравнения параболы  . Наименьшее значение
. Наименьшее значение  в области
в области  равно (-1), а наибольшее 0.
равно (-1), а наибольшее 0.
Область  снизу ограничена ветвью параболы
снизу ограничена ветвью параболы 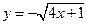 , а сверху прямой
, а сверху прямой  . Наименьшее значение
. Наименьшее значение  равно 0, наибольшее 8. Таким образом, двойной интеграл с измененным порядком интегрирования запишем в виде
равно 0, наибольшее 8. Таким образом, двойной интеграл с измененным порядком интегрирования запишем в виде
 .
.
Задача типа 8
Пример. Найти массу тонкой пластинки, ограниченной линиями 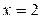 ;
;  ;
;  , поверхностная плотность которой равна
, поверхностная плотность которой равна  .
.
Решение. Построим фигуру, соответствующую данной пластинке.
 Масса плоской пластинки с поверхностной плотностью
Масса плоской пластинки с поверхностной плотностью  вычислим по формуле
вычислим по формуле

 ,
,
1) 
2)  (ед.массы)
(ед.массы)
 2020-06-12
2020-06-12 171
171








