Равномерная сходимость. Признак Вейерштрасса.
Определение. Будем говорить, что на множестве  задана функциональная последовательность
задана функциональная последовательность 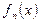 , если указано правило, по которому каждому натуральному числу ставится в соответствие функция, определенная на множестве
, если указано правило, по которому каждому натуральному числу ставится в соответствие функция, определенная на множестве  .
.
Определение. Функциональная последовательность 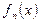 сходится в точке
сходится в точке  , если существует предел числовой последовательности
, если существует предел числовой последовательности  :
:  .
.
Определение*. Функциональная последовательность 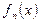 сходитсяк предельной функции
сходитсяк предельной функции  на множестве
на множестве  , если она сходится в каждой точке этого множества, т.е.
, если она сходится в каждой точке этого множества, т.е.  .
.
Определение. Пусть на множестве  задана функциональная последовательность
задана функциональная последовательность  . Выражение вида
. Выражение вида  называется функциональным рядом.
называется функциональным рядом.
Определение. Функциональный ряд  сходится на множестве
сходится на множестве  , если сходится последовательность его частичных сумм на
, если сходится последовательность его частичных сумм на  , т.е.
, т.е.  .
.
Пример. Пусть  ,
,  . Тогда при
. Тогда при  имеем:
имеем:  . Если
. Если  , то
, то  и
и  . Таким образом, последовательность
. Таким образом, последовательность 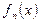 сходится к предельной функции
сходится к предельной функции  .
.
В этом примере предел последовательности непрерывных функций оказался разрывной функцией. Значит, непрерывность членов сходящейся на множестве  последовательности непрерывных функций не гарантирует непрерывности предельной функции. Чтобы разобраться в этом, рассмотрим более сильное понятие - понятие равномерной сходимости.
последовательности непрерывных функций не гарантирует непрерывности предельной функции. Чтобы разобраться в этом, рассмотрим более сильное понятие - понятие равномерной сходимости.
|
|
|
Определение. Последовательность 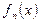 равномерно сходится к
равномерно сходится к  на множестве
на множестве  , если
, если  . Это обозначается так:
. Это обозначается так: 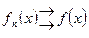 на
на  при
при  .
.
Отличие этого определения от определения* сходимости последовательности в том, что неравенство  при
при  должно выполняться сразу для всех
должно выполняться сразу для всех  .
.
Равномерная сходимость функционального ряда – это равномерная сходимость последовательности его частичных сумм  к сумме ряда
к сумме ряда  на
на  . Это равносильно тому, что
. Это равносильно тому, что  на
на  при
при  , т.е. остаток
, т.е. остаток  на
на  .
.
Приведем без доказательства критерий Коши равномерной сходимости последовательности.
Теорема. Последовательность 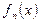 равномерно сходится к
равномерно сходится к  на множестве
на множестве  , тогда и только тогда, когда
, тогда и только тогда, когда 
 .
.
Из этой теоремы сразу следует критерий Коши равномерной сходимости функционального ряда.
Теорема. Ряд  равномерно сходится на множестве
равномерно сходится на множестве  , тогда и только тогда, когда
, тогда и только тогда, когда 
 .
.
Из критерия Коши следуют две теоремы – необходимое условие и достаточный признак равномерной сходимости ряда.
Теорема. (Необходимое условие сходимости ряда). Ряд  равномерно сходится на множестве
равномерно сходится на множестве  только тогда, когда
только тогда, когда  .
.
Действительно, полагая в критерии Коши  , получим:
, получим:
 , т.е.
, т.е.  .
.
Теорема. (Признак Вейерштрасса). Пусть  выполняется неравенство
выполняется неравенство  и пусть числовой ряд
и пусть числовой ряд  сходится. Тогда ряд
сходится. Тогда ряд  сходится на множестве
сходится на множестве  абсолютно и равномерно.
абсолютно и равномерно.
Доказательство. Достаточно проверить, что при условиях теоремы выполняется  . Но при любом
. Но при любом 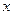 , при любых
, при любых  и
и  верно неравенство
верно неравенство
|
|
|
 .
.
А для ряда  с положительными членами выполняется необходимое условие Коши:
с положительными членами выполняется необходимое условие Коши: 
 .
.
Ряд  принято называть мажорантой (мажорантным рядом) для функционального ряда
принято называть мажорантой (мажорантным рядом) для функционального ряда  , а признак Вейерштрасса называют мажорантным признаком.
, а признак Вейерштрасса называют мажорантным признаком.
Пример 1. Ряд  равномерно (и абсолютно) сходится на
равномерно (и абсолютно) сходится на  . Действительно, при
. Действительно, при  имеет место оценка
имеет место оценка  , а ряд
, а ряд  сходится.
сходится.
Пример 2.  равномерно и абсолютно сходится на всей числовой прямой, т.к. для всех
равномерно и абсолютно сходится на всей числовой прямой, т.к. для всех  , а ряд
, а ряд  сходится.
сходится.
 2020-06-08
2020-06-08 249
249