Доказательство формулы бинома Ньютона

Бином Ньютона - формула.

Формула бинома Ньютона для натуральных n имеет вид 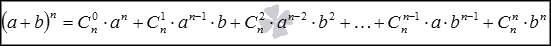, где 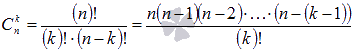- биномиальные коэффициенты, представляющие из себя сочетания из n по k, k=0,1,2,…,n, а "!" – это знак факториала).

К примеру, известная формула сокращенного умножения "квадрат суммы" вида 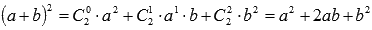есть частный случай бинома Ньютона при n=2.

Выражение, которое находится в правой части формулы бинома Ньютона, называют разложением выражения (a+b)ⁿ, а выражение 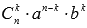называют (k+1) -ым членом разложения, k=0,1,2,…,n.

Треугольник Паскаля.

Биномиальные коэффициенты для различных n удобно представлять в виде таблицы, которая называется арифметический треугольник Паскаля. В общем виде треугольник Паскаля имеет следующий вид:

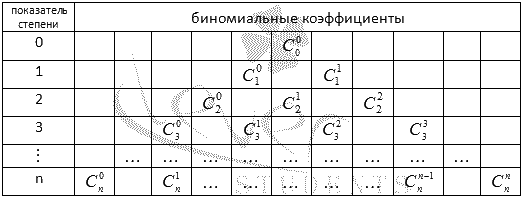
Треугольник Паскаля чаще встречается в виде значений коэффициентов бинома Ньютона для натуральных n:

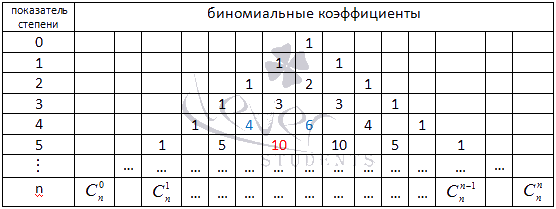
Боковые стороны треугольника Паскаля состоят из единиц. Внутри треугольника Паскаля стоят числа, получающиеся сложением двух соответствующих чисел над ним. Например, значение десять (выделено красным) получено как сумма четверки и шестерки (выделены голубым). Это правило справедливо для всех внутренних чисел, составляющих треугольник Паскаля, и объясняется свойствами коэффициентов бинома Ньютона.

Свойства биномиальных коэффициентов.

Для коэффициентов бинома Ньютона справедливы следующие свойства:

· коэффициенты, равноудаленные от начала и конца разложения, равны между собой , p=0,1,2,…,n;

· ;

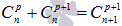· сумма биномиальных коэффициентов равна числу 2, возведенному в степень, равную показателю степени бинома Ньютона: ;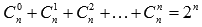

· сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме биномиальных коэффициентов, стоящих на нечетных местах.

Первые два свойства являются свойствами числа сочетаний.

Доказательство формулы бинома Ньютона.

Приведем доказательство формулы бинома Ньютона, то есть докажем справедливость равенства .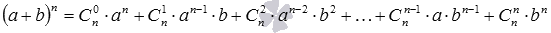

Воспользуемся для доказательства методом математической индукции.

1. Проверим справедливость разложения для какого-нибудь n, допустим, для n = 3.

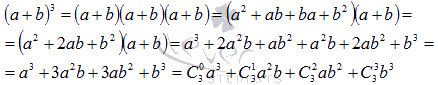
Получили верное равенство.

2. Предположим, что равенство верно для n-1, то есть, что справедливо равенство .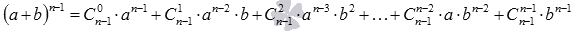

3. Докажем, что верно равенство 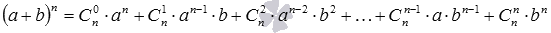, основываясь на предположении второго пункта.

Поехали!

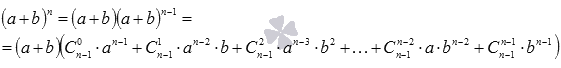
Раскрываем скобки

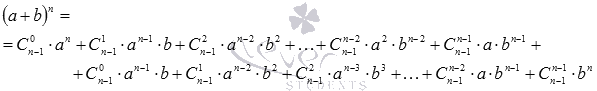
Группируем слагаемые

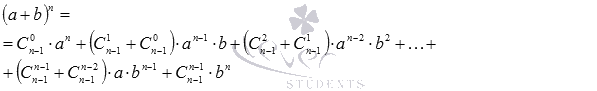
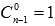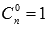Так как и , то 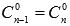; так как 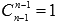и , то 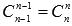; более того, используя свойство сочетаний 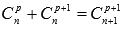, получим

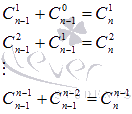
Подставив эти результаты в полученное выше равенство

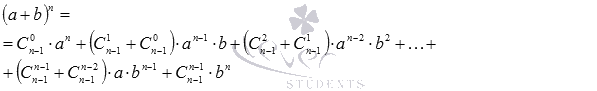
придем к формуле бинома Ньютона .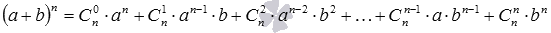

Этим доказана формула бинома Ньютона.

Общим термином «соединения» мы будем называть три вида комбинаций, составляемых из некоторого числа различных элементов, принадлежащих одному и тому же множеству (например, буквы алфавита, книги в библиотеке, машины на стоянке и т.д.).

Перестановки. Возьмём n различных элементов: a ₁, a ₂, a ₃, …, a_n. Будем переставлять их всеми возможными способами, сохраняя их количество и меняя лишь порядок их расположения. Каждая из полученных таким образом комбинаций называется перестановкой. Общее количество перестановок из n элементов обозначается P_n. Это число равно произведению всех целых чисел от 1 до n:

 

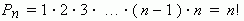
Символ n! (называется факториал) - сокращённая запись произведения: 1 · 2 · 3 · … · (n – 1) · n.

 

П р и м е р. Найти число перестановок из трёх элементов: a, b, c.

Р е ш е н и е. В соответствии с приведенной формулой: P ₃ = 1 · 2 · 3 = 6.
Действительно, мы имеем 6 перестановок: abc, acb, bac, bca, cab, cba.

Размещения. Будем составлять группы из m различных элементов, взятых из множества, состоящего из n элементов, располагая эти m взятых элементов в различном порядке. Полученные комбинации называются размещениями из n элементов по m.

Их общее количество обозначается: и равно произведению:

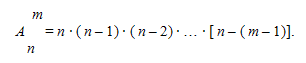
П р и м е р. Найти число размещений из четырёх элементов a, b, c, d по два.

Р е ш е н и е. В соответствии с формулой получим:

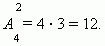
Вот эти размещения: ab, ba, ac, ca, ad, da, bc, cb, bd, db, cd, dc.

Сочетания. Будем составлять группы из m различных элементов, взятых из множества, состоящего из n элементов, не принимая во внимание порядок расположения этих m элементов. Тогда мы получим сочетания из n элементов по m.

Их общее количество обозначается 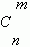и может быть вычислено по формуле:

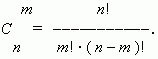
Из этой формулы ясно, что

 

Заметим, что можно составить только одно сочетание из n элементов по n, которое содержит все n элементов. Формула числа сочетаний даёт это значение, если только принять, что 0! = 1,что является определением 0!.

В соответствии с этим определением получим:

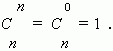
Общее число сочетаний можно вычислить, пользуясь и другим выражением:

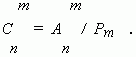
П р и м е р. Найти число сочетаний из пяти элементов: a, b, c, d, e по три.

Р е ш е н и е:

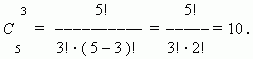
Эти сочетания: abc, abd, abe, acd, ace, ade, bcd, bce, bde, cde.

Бином Ньютона. Это формула, представляющая выражение (a + b) ⁿ при положительном целом n в виде многочлена:

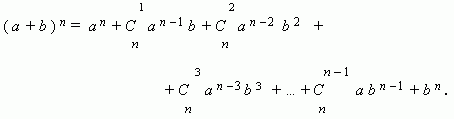
Заметим, что сумма показателей степеней для a и b постоянна и равна n.

П р и м е р 1.

Числа 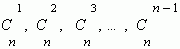называются биномиальными коэффициентами.

Их можно вычислить, применяя только сложение, если пользоваться следующей схемой. В верхней строке пишем две единицы. Все последующие строки начинаются и заканчиваются единицей. Промежуточные числа в этих строках получаются суммированием соседних чисел из предыдущей строки. Эта схема называется треугольником Паскаля:

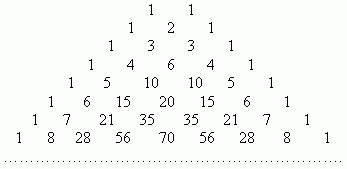
Первая строка в этой таблице содержит биномиальные коэффициенты для n = 1; вторая - для n = 2; третья - для n = 3 и т.д. Поэтому, если необходимо, например, разложить выражение:

(a + b)⁷,

мы можем получить результат моментально, используя таблицу:

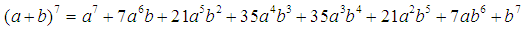
Свойства биномиальных коэффициентов.

1. Сумма коэффициентов разложения (a + b) ⁿ равна 2 ⁿ.

Для доказательства достаточно положить a = b = 1. Тогда в правой части разложения бинома Ньютона мы будем иметь сумму биномиальных коэффициентов, а слева:

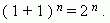
2. Коэффициенты членов, равноудалённых от концов разложения, равны.

Это свойство следует из соотношения:

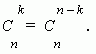
3. Сумма коэффициентов чётных членов разложения равна сумме коэффициентов нечётных членов разложения; каждая из них равна

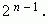
Для доказательства воспользуемся биномом: Здесь чётные члены имеют знак «+», а нечётные - «-». Так как в результате разложения получается 0, то следовательно, суммы их биномиальных коэффициентов равны между собой, поэтому каждая из них равна: что и требовалось доказать.