Условия интерференционного максимума и минимума

Тема 9. Волновая теория света. Интерференция света. Метод Юнга

Интерференцией волн называется явление усиления колебаний в одних точках пространства и ослабления колебаний в других точках в результате наложения двух или более волн, приходящих в эти точки. При наложении двух (или нескольких) световых волн происходит пространственное перераспределение светового потока, в результате чего в одних местах возникают максимумы, а в других – мини­мумы интенсивности. Необходимым условием наблюдения устойчивой интерференционной картины является когерентность складываемых волн. Когерентными называются волны одинаковой частоты, колебания в которых отличаются постоянной во времени разностью фаз.

Для получения когерентных световых волн применяют метод разделения волны, излучаемой одним источником, на две части, которые после прохождения разных оптических путей накладываются друг на друга, и в результате наблюдается интерференци­онная картина.

Произведение геомет­рической длины s пути световой волны в данной среде на показатель n преломления этой среды называется оптической длиной пути L, a величина D = L ₂ – L ₁ (разность оптических длин проходимых волнами путей) называется оптической разностью хода.

Если оптическая разность хода D равна целому числу длин волн l ₀, т.е.

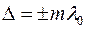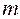(= 0, 1, 2,…),

то колебания, возбуждаемые в точке М обеими волнами, будут проис­ходить в одинаковой фазе, и в точке М будет наблюдаться интерференционный максимум (m – порядок интерференционного максимума).

Если же оптическая разность хода D равна полуцелому числу длин волн l ₀, т.е.

(= 0, 1, 2,…),

то колебания, возбуждаемые в точке М обеими волнами, будут проис­ходить в противофазе, и в точке М будет наблюдаться интерференционный минимум (m – порядок интерференционного минимума).

В качестве примера интерференции световых волн рассмотрим метод Юнга.

Метод Юнга. Для наблюдения интерференции света когерентные световые пучки получают разделением и последующим сведением световых лучей, исходящих из одного и того же источника. Источником света служит ярко освещенная щель S (рис. 20), от которой световая волна падает на две узкие равноудаленные щели S ₁ и S ₂, параллель­ные щели S. Таким образом, щели S ₁ и S ₂ играют роль когерентных источников, а интерференционная картина наблюдается на экране (Э), расположенном на некотором расстоянии l от щелей S ₁ и S ₂ (рис. 20). Щели S ₁ и S ₂ находятся на расстоянии d друг от друга (рис. 20), причем l >> d.

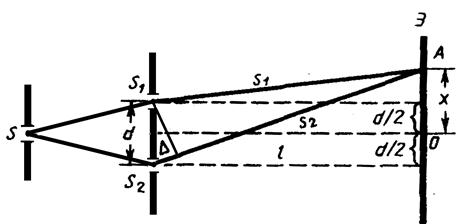
Рис. 20

Интерференция рассматривается в произ­вольной точке А на экране, расположенной на расстоянии x от точки O, симметричной от­носительно щелей и принятой за начало отсчета величины x.

Интенсивность света в точке А определяется оптической разностью хода лучей: D = s ₂ – s ₁ .

Согласно рисунку 20:

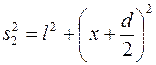; , откуда или .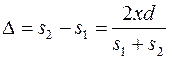

Из условия l >> d следует, что s ₁ + s ₂ » 2 l, тогда

.

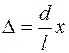Согласно этому соотношению и условиям наблюдения интерференционных максимумов и минимумов положения максимумов (x_max) и минимумов (x_min) интенсивности на экране в методе Юнга определяются следующим образом:

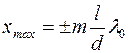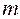(= 0, 1, 2,…),

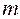(= 0, 1, 2,…).

Расстояние между двумя соседними максимумами (или минимумами) D x называется шириной интерференционной полосы и равно:

.

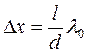Из этого соотношения следует, что величина D x зависит от длины волны l ₀ . Поэтому, четкая интерференционная картина, представляющая собой чередова­ние на экране светлых и темных полос, возможна только при использовании монохроматического света, то есть света определенной длины волны l ₀ .

Тема 10. Дифракция света. Дифракция Френеля

Дифракцией называется огибание волнами препятствий. Дифракцию света определяют как любое отклонение распространения света вблизи препятст­вий от законов геометрической оптики. Благодаря дифракции волны попадают в область геометрической тени, проникают через небольшие отверстия и т. д.

Явление дифракции объясняется с помощью принципа Гюйгенса, соглас­но которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта.

Согласно принципу Гюйгенса – Френеля световая волна, возбуждаемая каким-ли­бо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, «излучаемых» фиктивными источниками. Такими источниками могут служить, например, бесконечно малые элементы любой замкнутой поверхности, охватывающей источник S. Если в качестве таковой выбрать одну из волновых поверх­ностей (волновой поверхность – это геометрическое место точек, колебания в которых происходят в одинаковой фазе), то все бесконечно малые элементы этой замкнутой поверхности, как фиктивные источники, действуют синфазно. Это свойство фиктивных источников коге­рентных вторичных волн использовано в методе зон Френеля при изучении дифракции сферических волн.Френель дополнил принцип Гюйгенса идеей интерференции вторичных волн.

Метод зон Френеля. Найдем в произвольной точке М амплитуду световой волны, распространяющейся от точечного источника света S (рис. 21).

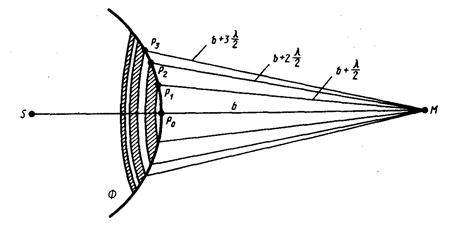
Френель разбил волновую поверхность Ф, являющуюся сферической поверхностью с центром в точке S, на кольцевые зоны (зоны Френеля) такого размера, чтобы расстояния от краев соседних зон до точки М отличались на l /2 (рис. 21). Так как колебания от соседних зон проходят до точки М расстояния, отличающиеся на l /2, то в точку М они приходят в противофазе и при наложении взаимно ослабляют друг друга. Поэтому амплитуда А результирующего колебания в точке М: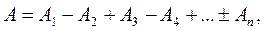

где А ₁, А ₂ ,..., А_n – амплитуды колебаний, идущих от 1-ой, 2-ой,..., n -ной зоны.

В результате сложения амплитуда А результирующего светового колебания в точке М оказалась равной половине амплитуды А ₁ центральной зоны Френеля:

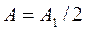. То есть, амплитуда светового колебания, идущего только от одной центральной зоны Френеля вдвое больше, чем амплитуда результирующего светового колебания при полностью открытом волновом фронте. Этот эффект подтвержден экс­периментально с помощью зонных пластинок, на практике, стеклянных пластинок, построенных по методу зон Френеля. Зонные пластинки состоят из чередующихся прозрачных (для нечетных зон Френеля) и непрозрачных (для четных зон Френеля) концентрических колец. В этом случае результирующая амплитуда А (A=A ₁ +A ₃ +A ₅ +...) больше, чем при полностью открытом волновом фронте. Опыт подтвердил, что зонные пластинки увеличивают освещенность в точке М, действуя подобно собирающей линзе.

Дифракция Френеля на круглом отверстии. Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути круглое отверстие (рис. 22). Дифрак­ционная картина на экране зависит от числа зон Френеля, открытых круглым отверстием. После разбиения открытой части волновой поверхности Ф на зоны Френеля для точки В, лежащей на экране (рис. 22), определяют число открытых зон. Если число открытых зон Френеля четное, то в точке В наблюдается темное пятно, так как колебания от каждой пары соседних зон Френеля взаимно гасят друг друга. Если же число открытых зон Френеля нечетное, то в точке В будет светлое пятно.

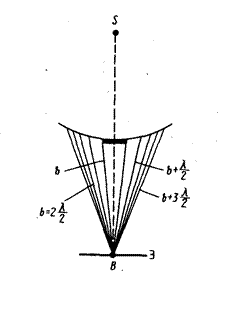
Дифракция Френеля на диске. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск (рис. 23). Пусть для точки В, лежащей на линии, соединяющей источник S с центром диска, после разбиения волновой поверхности Ф на зоны Френеля окажутся закрытыми диском m первых зон Френеля. Тогда амплитуда А результирующего колебания в точке В равна: 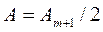, то есть в точке В будет светлое пятно, соответствующее действию поло­вины первой открытой зоны Френеля.