Интегрирование выражений, содержащих квадратный трехчлен

Интегральное исчисление функций одного переменного

 

Первообразная. Теоремы о первообразных. Неопределенный интеграл и его свойства. Таблица неопределенных интегралов.

 

Опр. Функция называется первообразной функции  на 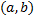, если .

Пример.  – первообразная функции  на интервале

Теорема 1 (об арифметических свойствах  первообразной).

Пусть  и  – первообразные функций  и  соответственно. Тогда функция  – первообразная функции  (  

Док-во: , т.е.  функция  – первообразная функции

Теорема 2 (об общем виде первообразной).

Пусть  – первообразная функции . Тогда любая первообразная функции  имеет вид

, где

Док-во: т.к. , то  – тоже первообразная функции . Покажем, что любая первообразная имеет вид . Пусть  – первообразная функции . Рассмотрим функцию : . Рассмотрим произвольные . т.е. . Значит,

Опр. Совокупность всех первообразных функции  называется неопределенным интегралом от функции .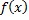

Обозн.: .

Пусть  – первообразная функции . Тогда , где 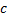 – произвольная постоянная.

Пример.

Свойства неопределенного интеграла:

1.

2.

3.   или

4. , где

Док-во:

1. , где  – первообразная функции

2. .

3. Т.к. 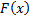 – первообразная , то .

4. Пусть  и  – первообразные функций  и  соответственно.

Тогда функция  – первообразная функции  (. Отсюда

Таблица интегралов:

1.

2. . (Т.к. при

3.   ()

4.

5.

6.

7.

8.

9.

10. ,

11. ,   (длинный логарифм)

12. ,

13. или (высокий логарифм)

14.

15.

16.

17.

Примеры.

 

Интегрирование подстановкой и по частям. Примеры. Интегрирование выражений, содержащих квадратный трехчлен. Интегрирование тригонометрических и иррациональных функций.

 

Подведение под знак дифференциала.

Пусть  – первообразная функции  на , т.е. . Рассмотрим замену , где  – дифференцируемая на 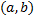 функция, .

Рассмотрим сложную функцию , .

, т.е.  – первообразная для , т.е. , или , или ,

                       

Примеры.

1.

2.

3. .

 

Замена переменной. Поменяем в (1.2.1) местами  и :  ,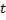

где  определена на ,  дифференцируема на , причем .

Пусть 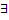 обратная функция  . Заменим 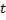 на :

Т.е.

Пример.

Интегрирование по частям

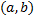Пусть функции  и  дифференцируемы на . Тогда , т.е.

Док-во: , т.е.

, т.е. ,

Примеры.

1. .

2. .

3. ,

 т.е. , т.е.

.

Интегрирование выражений, содержащих квадратный трехчлен

I.  , .

Выделим полный квадрат, получим табличный интеграл (10-13)

Примеры.

1. .

2. .

II. , .

Выделим в числителе производную квадратного трехчлена , т.е. представим числитель в виде

где  – находится с помощью выделения полного квадрата.

Аналогично

 

где  .

Примеры.

1.

2.