Векторная форма записи системы

Пусть . Тогда система (2.14.1) можно записать в виде

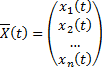Опр. Вектор-функция называется частным решением системы (2.14.1) на 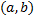, если при ее подстановке в (2.14.1) все уравнения системы (2.14.1) обращаются в тождества на .

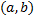Задача Коши для системы (1).

Найти частное решение 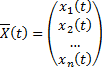, удовлетворяющее начальным условиям

где точка .

В векторной форме начальные условия имеют вид

где

Опр. Семейство вектор-функций , зависящих от 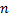произвольных постоянных, называется общим решением системы (2.14.1), если

1. вектор-функция является частным решением.

2. Для такие, что удовлетворяет начальному условию (2.14.2).

Векторная форма общего решения -

Теорема существования и единственности решения задачи Коши для нормальных систем.

Пусть функции и их частные производные непрерывны в области огда

Сведение ДУ n-го порядка к нормальной системе. Рассмотрим ДУ -го порядка

Введем обозначения:

Тогда уравнение (2.14.3) равносильно системе

Пример.

Сведение нормальной системы к одному уравнению n-го порядка.

Рассмотрим случай

Сведем к ДУ 2-го порядка. Из 1-го уравнения

Если из 1-го уравнения системы можно выразить , то для получим уравнение 2-го порядка:

(общее решение ДУ 2-го порядка).

Тогда .

Пример.
.

Продифференцируем 1-е уравнение:

Из 1-го уравнения:

Характеристическое уравнение полученного ЛОДУ с постоянными коэффициентами:

2.15.Автономные системы ДУ. Фазовое пространство и фазовые траектории. Первые интегралы систем ДУ. Симметричная форма записи систем ДУ и ее применение к нахождению первых интегралов.

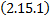– нормальная система ОДУ.

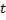– независимая переменная,

– независимые функции,

– определены в области .

Если не зависят явно от 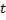, то система (2.15.1) является автономной.

Фазовая плоскость.

Рассмотрим

Пусть вектор-функция – частное решение автономной системы . Рассмотрим на плоскости кривую 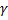, заданную параметрическими уравнениями

Кривая 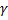– фазовая кривая системы на фазовой плоскости . Если система удовлетворяет условию теоремы существования и единственности, т.е. имеют непрерывные частные производные первого порядка в области , то через каждую точку области 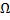проходит ровно одна фазовая кривая.