2020-09-24
214
Рассмотрим дискретную случайную величину X, закон распределения которой неизвестен. Пусть произведено n испытаний, в которых величина X приняла 
раз значение 
, 
раз значение 
, …, 
раз значение 
, причем 
.
Эмпирическими частотами называют фактически наблюдаемые частоты 
.
Пусть имеются основания предположить, что изучаемая случайная величина X распределена по некоторому определенному закону. Чтобы проверить, согласуется ли это предположение с данными наблюдений, вычисляют частоты наблюдаемых значений, т. е. находят теоретически частоту 
каждого из наблюдаемых значений в предположении, что величина X распределена по предполагаемому закону.
Выравнивающими (теоретическими) частотами в отличие от фактически наблюдаемых эмпирических частот называют частоты , найденные теоретически (вычислением). Выравнивающие частоты находят с помощью равенства
,
где n – число испытаний; 
– вероятность наблюдаемого значения 
, вычисленная при допущении, что X имеет предполагаемое распределение.
Итак, выравнивающая частота наблюдаемого значения дискретного распределения равна произведению числа испытаний на вероятность этого наблюдаемого значения.
В случае непрерывного распределения, вероятности отдельных возможных значений равны нулю. Поэтому весь интервал возможных значений делят на k непересекающихся интервалов и вычисляют вероятности попадания X в i -й частичный интервал, а затем, как и для дискретного распределения, умножают число испытаний на эти вероятности.
Итак, выравнивающие частоты непрерывного распределения находят по равенству
,
где n – число испытаний; – вероятность попадания X в i -й частичный интервал, вычисленная при допущении, что X имеет предполагаемое распределение.
Если имеются основания предположить, что случайная величина X (генеральная совокупность) распределена нормально, то выравнивающие частоты могут быть найдены по формуле
,
где n – число испытаний (объем выборки), h – длина частичного интервала,
s – исправленное выборочное среднее квадратическое отклонение, 
( – середина i -ого частичного интервала), а значение функции 
находят по таблице прил. 2.
Замечание 1
1) При использовании таблицы для вычисления значений функции 
следует учитывать, что эта функция четная, т. е. 
.
2) Чтобы пользоваться таблицей значений функции , достаточно
вычислять числа 
с двумя знаками после запятой.
3) Числа 
округлены до целых.
Если эмпирическое распределение задано в виде последовательности интервалов и соответствующих им частот, то для вычисления теоретических частот нормально распределенной случайной величины можно воспользоваться более точными формулами
,
где 
, 
, 
- левый, а 
- правый концы i -ого частичного интервала разбиения, 
- функция Лапласа, значения которой находятся по таблице прил. 1.
Замечание 2
1) При использовании таблицы для вычисления значений функции следует учитывать, что эта функция нечетная, т. е. 
= – .
2) Чтобы пользоваться таблицей значений функции , достаточно
вычислять числа 
и 
с двумя знаками после запятой.
3)Числа округлены до целых.
Пример 12.1. Из генеральной совокупности извлечена выборка объема.
| Варианты |
| 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 |
| Частоты |
| 6 | 13 | 38 | 74 | 106 | 85 | 30 | 10 | 4 |
Построить полигон частот и нормальную кривую по данному распределению.
Решение.
С целью упрощения вычислений перейдем к условным вариантам 
, где 
, 
. Результаты вычислений оформим в виде таблицы
Т а б л и ц а 12.1
|
|
| 
| 
| 
|
| 15 | 6 | - 4 | - 24 | 96 |
| 20 | 13 | - 3 | - 39 | 117 |
| 25 | 38 | - 2 | - 76 | 152 |
| 30 | 74 | - 1 | - 74 | 74 |
| 35 | 106 | 0 | 0 | 0 |
| 40 | 85 | 1 | 85 | 85 |
| 45 | 30 | 2 | 60 | 120 |
| 50 | 10 | 3 | 30 | 90 |
| 55 | 4 | 4 | 16 | 64 |
| 
| 
|
Тогда
,
,
,
,
.
Вычислим выравнивающие частоты (табл. 12.2)
Т а б л и ц а 12.2
|
|
| 
| 
| 
| 
|
| 15 | 6 | - 19,7 | - 2,67 | 0,0113 | 3 |
| 20 | 13 | - 14,7 | - 1,99 | 0,0551 | 14 |
| 25 | 38 | - 9,7 | - 1,31 | 0,1691 | 42 |
| 30 | 74 | - 4,7 | - 0,63 | 0,3271 | 82 |
| 35 | 106 | 0,3 | 0,05 | 0,3984 | 99 |
| 40 | 85 | 5,3 | 0,73 | 0,3056 | 76 |
| 45 | 30 | 10,3 | 1,41 | 0,1476 | 37 |
| 50 | 10 | 15,3 | 2,09 | 0,0449 | 11 |
| 55 | 4 | 20,3 | 2,77 | 0,0086 | 2 |
| n =366 |  = 366
|
Первый и последний столбцы табл. 12.2 дают координаты точек (, 
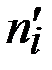), по которым строится кривая нормального распределения.
Рис. 12.1
Близость теоретических и эмпирических частот говорит в пользу предположения о нормальном законе заданного распределения.
На рис. 12.1 построены нормальная (теоретическая) кривая по выравнивающим частотам (они отмечены крестиками) и полигон наблюдаемых частот (они отмечены точками). Сравнение графиков наглядно показывает, что построенная теоретическая кривая удовлетворительно отражает данные наблюдений. Для того чтобы более уверенно считать, что данные наблюдений свидетельствуют о нормальном распределении признака, пользуются специальными правилами, которые называют критериями согласия.
