Теоремы. Пусть относительно прямоугольно-декартовой системы координат в пространстве заданы плоскость  и прямая
и прямая  . Тогда:
. Тогда:
1.  , если
, если  ;
;
2. 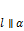 , если
, если  и
и  ;
;
3.  , если
, если  и
и  .
.
Прямая как линия пересечения двух плоскостей. Теорема
Пусть относительно прямоугольно-декартовой системы координат заданы две плоскости:
 и
и 
 .
.
Теорема.  задаётся своим каноническим уравнением
задаётся своим каноническим уравнением  , где
, где  .
.
Геометрический смысл неравенства первой степени с тремя неизвестными
Плоскость  делит пространство на два полупространства:
делит пространство на два полупространства:
· ( ) положительно-ориентированное;
) положительно-ориентированное;
· ( ) отрицательно-ориентированное.
) отрицательно-ориентированное.
Расстояние от точки до плоскости в пространстве. Теорема
Теорема. Заданы:  и
и  . Расстояние
. Расстояние  от
от  до
до  определяется по формуле:
определяется по формуле:

Доказательство:
· возьмём на  произвольным образом точку на плоскости
произвольным образом точку на плоскости  и составим вектор
и составим вектор  ;
;
·  ;
;
· расстояние  от точки
от точки  до
до  равно проекции
равно проекции  на
на  ;
;
· С другой стороны,  , где
, где  – угол между
– угол между  ;
;
· 
·  – перпендикуляр к плоскости, рассмотрим прямоугольный треугольник, в котором
– перпендикуляр к плоскости, рассмотрим прямоугольный треугольник, в котором 
|
|
|
· 
· 
·  (а значит
(а значит  )
)
· 
Угол между двумя плоскостями. Условие перпендикулярности и параллельности двух плоскостей
Пусть относительно прямоугольно-декартовой системы координат заданы 2 плоскости:
 и
и 
Углом между  и
и  называют угол между векторами
называют угол между векторами  и
и  , перпендикулярными
, перпендикулярными  и
и  соответсвенно:
соответсвенно:

Из этой формулы следует, что:
1.  когда
когда  ;
;
2.  когда
когда 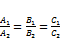 .
.
Нормальное уравнение прямой в пространстве

Угол между двумя прямыми в пространстве. Условие перпендикулярности и параллельности двух прямых в пространстве
Пусть относительно прямоугольно-декартовой системы координат заданы две прямые своими каноническими уравнениями:
 и
и 
Тогда  и
и  – направляющие векторы
– направляющие векторы 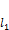 и
и  соответственно.
соответственно.
Углом между прямыми называют угол между направляющими векторами. Справедлива формула:
 .
.
Из этой формулы следует, что:
1.  , когда
, когда  ;
;
2. 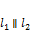 , когда
, когда  .
.
 2020-09-24
2020-09-24 162
162








