Решение задачи на равновесие сил

1. Пару сил можно уравновесить только парой сил. Поэтому в точках С и D к стержню необходимо приложить две равные силы так, чтобы они образовали пару сил с моментом, равным моменту пары (Р_A, P_B), но имеющим противоположный знак.

Так как пара (Р_A, P_B) поворачивает стержень по ходу часовой стрелки, искомые силы должны поворачивать его против хода часовой стрелки (рис. 68, б).

2. Применяем условие равновесия:
M_AB + M_CD = 0.
Или, подставив значения моментов,
-P_A * AE + P_C * CD = 0,
где
AE = AB cos α.

Отсюда
P_C = P_A * AE / CD = 100*3*cos 60° / 1 = 150 н.

Следовательно, в точках С и D необходимо приложить силы Р_C и P_D по 150 н каждая, как показано на рис. 68, б.

Условие задачи Определить моменты шести заданных сил (рис. 71) относительно точек А, В и С, если Р1=30 н, Р2=50 н, Р3=25 н, Р4=40 н, Р5=35 н, Р6=54 н, AB=1,2 м, BC=0,8 м, α=55° и β=35°. << задача 55 || задача 58 >>

В задаче 57 силы расположены так, что либо их плечи определяются очень просто – как катеты прямоугольных треугольников, в которых даны гипотенузы, либо плечи заданы в условии задачи (ВС и АС).

Но иногда некоторые силы заданной системы оказываются расположенными относительно выбранного центра моментов так, что определить длину плеча трудно и требуется, например, предварительно вычислить длины еще одного-двух отрезков. В таких случаях целесообразно силу разложить на две составляющие и применить для определения ее момента теорему Вариньона (§ 28 в учебнике Е. М. Никитина).

Условие задачи Определить моменты относительно точки А сил Р1=40 н, Р2=60 н, Р3=30 н и Р4=50 н, приложенных в точках А, В и С, как показано на рис. 72, а. Углы α=30°, β=50°, AB=2,5 м, ВС=1,5 м. << задача 57 || задача 60 >>

Вариант 2-й. Чтобы избежать определения плеча АЕ, которое в данном случае находится после предварительного вычисления двух отрезков (FB и AF), необходимо момент силы Р₄ относительно точки А найти по теореме Вариньона: момент равнодействующей плоской системы сил относительно любой точки, лежащей в той же плоскости, равен алгебраической сумме моментов составляющих сил относительно той же точки.

Разложим силу Р₄ на две составляющие: одну, направленную вдоль отрезка ВС, и другую – перпендикулярно к нему (рис. 72, б).

Модуль первой составляющей Р₄ cos β, а ее плечо – отрезок АВ, длина которого задана. Модуль второй составляющей Р₄ sin β, а ее плечо АК=ВС=1,5 м.

Применяя теорему Вариньона, получаем
M_A(Р₄) = Р₄ cos β * AB - Р₄ sin β * AK = Р₄(AB cos β - BC sin β).

Как видно, получено точно такое же значение момента, что и в первом варианте решения:
M_A(Р₄) = 23 н*м.

Условие задачи К точкам A, B, C и D, образующим прямоугольник со сторонами АВ=80 см и ВС=180 см, приложены пять сил, как показано на рис. 75, а. Определить главный вектор и главный момент этой системы сил, если Р1=50 н, Р2=74 н, Р3=60 н, P4=40 н, Р5=51 н и угол α=60°. При определении главного момента центр приведения выбрать наиболее рациональным образом. << задача 58 || задача 61 >>

Решение задачи

1. Примем за центр приведения точку А (в этой точке пересекаются линии действия трех сил из пяти) и ее же примем за начало координат, совместив ось х со стороной АВ прямоугольника, а ось у – со стороной DA.

2. Найдем проекции всех заданных сил на ось х:

Таким образом, вследствие удачного выбора центра приведения сразу определяется равнодействующая R: ее модуль R=66,5 н, линия ее действия MN проходит через точку А под углом φ_x=45° к стороне АВ.

Если за центр приведения выбрать другую точку, то главный момент не получится равным нулю, кроме тех случаев, когда выбранная точка оказывается на линии действия равнодействующей.

Условие задачи К вершинам квадрата ABCD приложены шесть сил, как показано на рис. 76, а. Сторона квадрата 1 м, модули сил Р1=Р4=100 н, Р2=40 н, Р3=Р5=113 н и Р6=120 н. Определить главный вектор и главный момент данной системы сил относительно точки D. << задача 60 || задача 62 >>

Решение задачи

1. Поместим начало осей координат в точке D (см. рис. 76, а).

2. Найдем проекции всех сил на ось х:

В задаче рассмотрена система сил, приводящаяся к паре сил. В связи с этим необходимо обратить внимание на два очень важных свойства пары:

а) алгебраическая сумма проекций сил, составляющих пару, на любую ось равна нулю;

б) алгебраическая сумма моментов сил, образующих пару относительно любой точки, лежащей в плоскости действия пары, есть величина постоянная, равная моменту пары (Е. М. Никитин, § 22).

Действительно, допустим, что на рис. 76 имеются только две силы P₁ и P₄ (причем P₁=P₄=100 н). При любом расположении осей х и у
X₁ + X₄ = 0 и Y₁ + Y₄ = 0.

(Рекомендуется проверить самостоятельно справедливость этих равенств при расположении осей, заданном на рис. 76, а также совместив оси х и у с диагоналями квадрата ABCD.) При любом положении центра моментов
M(P₁) + M(P₄) = 100 н*м.

(Рекомендуется проверить и это равенство, приняв за центр моментов любую из точек A, В, С, D или точку пересечения диагоналей квадрата, или любую другую.)

Именно поэтому пара сил, действующая на тело, обычно задается в виде момента и изображается круговой стрелкой, показывающей направление действия момента.

Отмеченные здесь свойства пары постоянно используются при составлении уравнений равновесия в задачах, рассмотренных в § 14:

а) при составлении уравнений проекций силы, образующие пару, не учитываются (сумма их проекций всегда равна нулю);

б) при составлении уравнений моментов момент пары сил входит в уравнение независимо от того, где выбран центр моментов.

Условие задачи К четырем точкам тела, образующим квадрат ABCD со стороной 1,2 м приложены силы Р1=5 кн, Р2=2 кн, Р3=3 кн и Р4=4 кн, как показано на рис. 77, а. Определить равнодействующую этой системы сил. << задача 61 || задача 65 >>

Решение задачи

1. За центр приведения примем точку А. Оси координат совместим со сторонами АВ и AD квадрата ABCD (рис. 77, а).

2. Найдем проекции сил на ось х:

Отрезок АЕ отложим перпендикулярно к направлению R_гл, причем в такую сторону, чтобы приложенная к точке Е равнодействующая сила R стремилась повернуть АЕ в направлении действия главного момента.

Таким образом, равнодействующая данных четырех сил численно равна 2,83 кн, направлена перпендикулярно к диагонали АС и линия ее действия находится от вершины A квадрата на расстоянии АЕ=2,12 м.

Условие задачи Определить равнодействующую двух параллельных сил Р1 и Р2, направленных в одну сторону (рис. 81, а), если Р1=12 н и Р2=15 н. << задача 62 || задача 66 >>

Решение задачи

1. Примем за начало осей проекций точку А. Ось х расположим перпендикулярно к данным силам и направим ее вправо, а ось у направим вдоль силы Р₁ вниз (рис. 81, б).

2. Найдем модуль равнодействующей:
∑ Y_i = Р₁ + Р₂ = 12 + 15 = 27.

Следовательно, R = 27 н.

Так как сумма проекций положительна, то вектор равнодействующей направлен тоже вниз.

3. Приняв за центр моментов точку А, найдем расстояние АС от точки A до линии действия равнодействующей.

В данном случае
M_A(R) = M_A(P₁) + M_A(P₂),
но
M_A(R) = -R * AC; M_A(P₁) = 0 и M_A(P₂) = -P₂ * AB,
поэтому
R * AC = P₂ * AB.
Откуда
AC = P₂ * AB / R = 15 * 1,8 / 27 = 1 м.

Таким образом, равнодействующая двух данных сил численно равна 27 н, и линия ее действия расположена от точки A на расстоянии AC=1 м (рис. 81, в).

Условие задачи Найти равнодействующую двух параллельных сил Р1 и Р2, направленных в разные стороны, если Р1=12 кн и Р2=60 кн (рис. 82, а). << задача 65 || задача 67 >>

Решение задачи

1. Расположим оси Ox и Oy так, как показано на рис. 82, б.

2. Найдем модуль равнодействующей:
∑ X_i = Р₁ - Р₂ = 12 - 60 = -48.

Следовательно, R = 48 н.

Сумма проекций заданных сил имеет отрицательное значение. Следовательно, равнодействующая направлена влево (ось Ох направлена вправо).

3. Приняв за центр моментов точку O и предположив, что линия действия R пересекает отрезок ОВ в точке A, составим уравнение Вариньона:
R * OA = -Р₁ * OB.
Отсюда
OA = -Р₁ * OB / R = -12 * 1 / 48 = -0,25 м.

Числовое значение OA получается отрицательным, значит этот отрезок от точки О необходимо отложить в противоположную сторону от ранее предполагаемого.

Равнодействующая заданных сил численно равна 48 н, направлена влево, и линия ее действия лежит ниже точки О на 0,25 м (рис. 82, в).

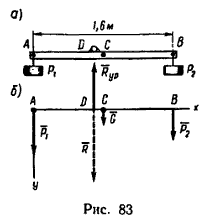
Условие задачи К концам прямолинейной однородной планки длиной 1,6 м и весом 5 н прикреплены два груза (рис. 83): слева – груз Р1=20 н, справа – Р2=15 н. В каком месте планки нужно приделать петельку, чтобы подвешенная на ней планка с грузами оставалась в горизонтальном положении? << задача 66 || задача 68 >>

Решение задачи

1. Изобразим на рис. 83 в горизонтальном положении планку АВ с грузами Р₁=20 н и Р₂=15 н. Так как планка однородная, ее вес G=5 н приложен в середине (в точке С).

Таким образом, к планке приложена система трех параллельных сил, действующих в одну сторону (рис. 83, б).

2. Оси проекций расположим, как показано на рис. 83, б.

3. Найдем модуль равнодействующей сил Р₁, Р₂ и G:
∑ Y_i = Р₁ + G + Р₂ = 20 + 5 + 15 = 40,
R = 40 н.

Равнодействующая направлена вертикально вниз.

4. Определим, на каком расстоянии AD от точки А (левого конца планки) расположена линия действия равнодействующей:
-R * AD = - G * AC - Р₂ * AB.
Отсюда
AD= (G*AC + Р₂*AB)/R = (5*0,8 + 15*1,6)/40 = 0,7 м.

Линия равнодействующей проходит через точку D на расстоянии 0,7 м от левого конца планки.

В этом месте и необходимо прикрепить к планке петельку. Если теперь за петельку подвесить планку на гвоздь или прикрепить к нити, то планка будет находиться в равновесии, оставаясь горизонтальной, так как равнодействующая R уравновесится реакцией R_ур гвоздя или нити.

Условие задачи Балансир AB, на который действуют пять горизонтально направленных параллельных сил (рис. 84), должен находиться в равновесии в вертикальном положении, будучи насаженным на горизонтальную ось. Определить, где необходимо поместить ось балансира, пренебрегая его весом. << задача 67 || задача 70 >>

Решение задачи

1. Расположив оси проекций, как указано на рис. 84, найдем модуль равнодействующей системы параллельных сил:
∑ X_i = Р₁ - Р₂ + Р₃ + Р₄ - Р₅ = 10 - 16 + 15 + 8 - 8 = 9,
R = 9 кн.

Таким образом, равнодействующая направлена вправо.

2. Определим расстояние ВО от нижнего конца балансира до линии действия R из уравнения Вариньона (центр моментов в точке В):
-R*BO = -Р₁*BA + Р₂*BC - Р₃*BD - Р₄*BE.
Отсюда
BO = (Р₁*BA - Р₂*BC + Р₃*BD + Р₄*BE)/R = (10*90 - 16*70 + 15*40 + 8*25)/9 = 64,5 см.

Следовательно, линия действия равнодействующей пересекает находящийся в вертикальном положении балансир на расстоянии 64,5 см от нижнего конца В. Здесь (в точке О) и нужно поместить ось балансира

Условие задачи Масса неоднородного стержня составляет 4,5 кг. Для определения положения центра тяжести стержня его левый конец положен на гладкую опору, а правый зацеплен крюком динамометра (рис. 86, а). При горизонтальном положении стержня динамометр показывает усилие 1,8 кГ. Расстояние АВ=130 см от левой опоры до динамометра определено путем непосредственного измерения. Определить положение центра тяжести стержня. << задача 68 || задача 71 >>

Решение задачи

1. Рассмотрим стержень как рычаг с опорой в точке А. Кроме реакции опоры, на него действуют две нагрузки: вес G=4,5 кГ (1 кг массы притягивается к земле силой, равной 1 кГ), приложенный в центре тяжести на искомом расстоянии х от опоры А, и усилие пружины динамометра Р=1,8 кГ (рис. 86, б).

2. Составим уравнение равновесия рычага:
∑ M_A(P_i) = 0,

В данном случае относительно точки А моменты создают две силы Р и G:
M_A(P) = +P * AB и M_A(G) = -Gx.

Следовательно,
P * AB - Gx = 0.

Решаем полученное уравнение:
x = P * AB / G = 1,8 * 130 / 4,5 = 52 см.

Центр тяжести стержня расположен на расстоянии 52 см от левой опоры.

 

Задачу 23 просто решить графическим методом. Для этого нужно начертить в масштабе расположение нитей и, выбрав масштаб для сил (например, 0,2 кГ/мм), построить на векторе G силовой треугольник и, измерив его стороны, найти T_A и T_B (графическое решение рекомендуется выполнить самостоятельно).

Графо-аналитический метод с использованием свойств подобных треугольников целесообразно применять к решению таких задач в том случае, если в схеме конструкции или устройства имеется треугольник, подобный силовому.

Если же в схеме конструкции нет треугольника, подобного силовому, то решение графо-аналитическим методом целесообразнее производить с использованием тригонометрических свойств, потому что при наличии линейных размеров необходимые для решения задачи значения углов, как правило, найти очень просто.

Необходимо отметить, что в задачах, подобных 22 и 23, усилия, вызываемые нагрузкой в стержнях кронштейнов или нитях устройств, удерживающих груз, не зависят от длины этих нитей или стержней.

Допустим, что груз (задача 23) удерживается нитями, прикрепленными не к вертикальной стенке и горизонтальному потолку, как на рис. 30, а к двум точкам криволинейной (сводчатой) поверхности (рис. 32). Но если при этом углы α и β, образуемые нитями CB и CA с вертикалью, остаются такими же, как и на рис. 30, то усилия T_A к T_B не изменяются, хотя сами нити в данном случае становятся короче.