Раскраской вершин графа называется назначение цветов его вершинам. Раскраска называется правильной, если любые две смежные вершины имеют разные цвета. Задача о раскраске состоит в нахождении правильной раскраски данного графа G в наименьшее число цветов. Это число называется хроматическим числом графа и обозначается  .
.
В правильной раскраске полного графа  все вершины должны иметь разные цвета, поэтому
все вершины должны иметь разные цвета, поэтому  . Если в каком-нибудь графе имеется полный подграф с k вершинами, то для раскраски этого подграфа необходимо k цветов. Отсюда следует, что для любого графа выполняется неравенство
. Если в каком-нибудь графе имеется полный подграф с k вершинами, то для раскраски этого подграфа необходимо k цветов. Отсюда следует, что для любого графа выполняется неравенство
 .
.
Однако хроматическое число может быть и строго больше кликового числа. Например, 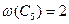 , а
, а 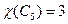 .
.
Раскраску можно также рассматривать как разбиение множества вершин на независимые множества. Каждая из частей разбиения представляет собой множество вершин одного цвета, эти множества называют цветными классами. Каждый цветной класс содержит не более чем 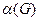 вершин. Поэтому произведение числа классов (т.е. цветов) на
вершин. Поэтому произведение числа классов (т.е. цветов) на 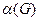 не превосходит числа всех вершин графа. Отсюда следует неравенство
не превосходит числа всех вершин графа. Отсюда следует неравенство
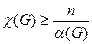 .
.
Тот же граф  служит примером, когда это неравенство строгое.
служит примером, когда это неравенство строгое.
Очевидно,  тогда и только тогда, когда G – пустой граф. Нетрудно охарактеризовать и графы с хроматическим числом 2 (точнее, не больше 2). По определению, это такие графы, у которых множество вершин можно разбить на два независимых множества. Но это совпадает с определением двудольного графа. Поэтому двудольные графы называют еще бихроматическими. Согласно теореме Кёнига, граф является бихроматическим тогда и только тогда, когда в нем нет циклов нечетной длины.
тогда и только тогда, когда G – пустой граф. Нетрудно охарактеризовать и графы с хроматическим числом 2 (точнее, не больше 2). По определению, это такие графы, у которых множество вершин можно разбить на два независимых множества. Но это совпадает с определением двудольного графа. Поэтому двудольные графы называют еще бихроматическими. Согласно теореме Кёнига, граф является бихроматическим тогда и только тогда, когда в нем нет циклов нечетной длины.
Для графов с хроматическим числом 3 такого простого описания не найдено. Не известны и простые алгоритмы, проверяющие, можно ли данный граф раскрасить в 3 цвета. Задача такой проверки (вообще, задача проверки возможности раскрасить граф в k цветов при любом фиксированном  ) относится к неподдающимся.
) относится к неподдающимся.
Рассмотрим алгоритм решения задачи о раскраске, похожий на описанный выше алгоритм для задачи о независимом множестве. Сходство заключается в том, что задача для данного графа сводится к той же задаче для двух других графов. Поэтому снова возникает дерево решений, обход которого позволяет найти решение. Но есть и одно существенное различие, состоящее в том, что теперь два новых графа не будут подграфами исходного графа.
Выберем в данном графе G две несмежные вершины x и y и построим два новых графа: 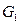 , получающийся добавлением ребра
, получающийся добавлением ребра 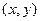 к графу G, и
к графу G, и 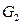 , получающийся из G слиянием вершин x и y. Операция слияния состоит в удалении вершин x и y и добавлении новой вершины z и ребер, соединяющих ее с каждой вершиной, с которой была смежна хотя бы одна из вершин x, y.
, получающийся из G слиянием вершин x и y. Операция слияния состоит в удалении вершин x и y и добавлении новой вершины z и ребер, соединяющих ее с каждой вершиной, с которой была смежна хотя бы одна из вершин x, y.
Если в правильной раскраске графа G вершины x и y имеют разные цвета, то она будет правильной и для графа 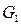 . Если же цвета вершин x и y в раскраске графа G одинаковы, то граф
. Если же цвета вершин x и y в раскраске графа G одинаковы, то граф  можно раскрасить в то же число цветов: новая вершина z окрашивается в тот цвет, в который окрашены вершины x и y, а все остальные вершины сохраняют те цвета, которые они имели в графе G. И наоборот, раскраска каждого из графов
можно раскрасить в то же число цветов: новая вершина z окрашивается в тот цвет, в который окрашены вершины x и y, а все остальные вершины сохраняют те цвета, которые они имели в графе G. И наоборот, раскраска каждого из графов 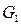 ,
,  , очевидно, дает раскраску графа G в то же число цветов. Поэтому
, очевидно, дает раскраску графа G в то же число цветов. Поэтому
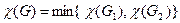 ,
,
что дает возможность рекурсивного нахождения раскраски графа в минимальное число цветов. Заметим, что граф 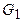 имеет столько же вершин, сколько исходный граф, но у него больше ребер. Поэтому рекурсия в конечном счете приводит к полным графам, для которых задача о раскраске решается тривиально.
имеет столько же вершин, сколько исходный граф, но у него больше ребер. Поэтому рекурсия в конечном счете приводит к полным графам, для которых задача о раскраске решается тривиально.
Для задачи о раскраске вершин придумано немало эвристик. Одна из простейших называется последовательной раскраской. Вершины графа как-нибудь линейно упорядочиваются и раскрашиваются в этом порядке в цвета, которыми являются натуральные числа. Очередная вершина красится в наименьший цвет, который еще не использован ни для одной из смежных с ней вершин. Интересно, что для любого графа существует упорядочение, при котором последовательная раскраска дает оптимальный результат.
Обозначим через 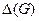 наибольшую степень вершины в графе
наибольшую степень вершины в графе 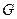 . При окрашивании очередной вершины в алгоритме последовательной раскраски для смежных с ней вершин использовано не более
. При окрашивании очередной вершины в алгоритме последовательной раскраски для смежных с ней вершин использовано не более 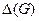 цветов, значит, хотя бы один из цветов
цветов, значит, хотя бы один из цветов 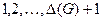 свободен и может быть применен. Отсюда следует еще одно неравенство для хроматического числа:
свободен и может быть применен. Отсюда следует еще одно неравенство для хроматического числа:
 ,
,
причем алгоритм последовательной раскраски в любом случае использует не более 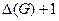 цветов.
цветов.
 2014-02-04
2014-02-04 1982
1982








