Метод увеличивающих путей
Пусть G – граф, М – некоторое паросочетание в нем. Ребра паросочетания будем называть сильными, остальные ребра графа – слабыми. Вершину назовем свободной, если она не принадлежит ребру паросочетания. Чередующимся путем относительно данного паросочетания называется простой путь, в котором чередуются сильные и слабые ребра (т.е. за сильным ребром следует слабое, за слабым – сильное). Чередующийся путь называется увеличивающим путем, если он соединяет две свободные вершины. Если имеется увеличивающий путь относительно данного паросочетания, то можно построить большее паросочетание – нужно вдоль этого пути превратить слабые ребра в сильные, а сильные в слабые. Эту операцию назовем инверсией. В результате инверсии мощность паросочетания увеличивается на 1.
Теорема об увеличивающем пути. Паросочетание является наибольшим тогда и только тогда, когда относительно него нет увеличивающих путей.
Для решения задачи о паросочетании остается научиться находить увеличивающие пути или убеждаться, что таких путей нет. Это можно сделать, перебирая чередующиеся пути (подобно перебору путей при поиске гамильтонова цикла). Дело осложняется тем, что чередующихся путей может быть много (см. задачу 7.4). Оказывается, нет необходимости перебирать их все. Известны эффективные алгоритмы, которые ищут увеличивающие пути для произвольных графов. Рассмотрим простой алгоритм, решающий эту задачу для двудольных графов.
Пусть 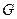 – двудольный граф c долями A и B, М – паросочетание в G. Всякий увеличивающий путь, если такой имеется, соединяет вершину из множества A с вершиной из B. Поэтому при поиске увеличивающего пути достаточно рассматривать чередующиеся пути, начинающиеся в свободных вершинах из доли А.
– двудольный граф c долями A и B, М – паросочетание в G. Всякий увеличивающий путь, если такой имеется, соединяет вершину из множества A с вершиной из B. Поэтому при поиске увеличивающего пути достаточно рассматривать чередующиеся пути, начинающиеся в свободных вершинах из доли А.
Зафиксируем некоторую свободную вершину 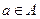 . Дерево Т с корнем в вершине a назовем деревом достижимости для вершины а, если
. Дерево Т с корнем в вершине a назовем деревом достижимости для вершины а, если
1) Т является подграфом графа 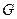 ;
;
2) каждый путь в дереве Т, начинающийся в корне, является чередующимся путем;
3) Т – максимальное дерево со свойствами 1) и 2).
Дерево достижимости определено не однозначно, но любое такое дерево в двудольном графе обладает следующим свойством.
Теорема о дереве достижимости. Пусть G – двудольный граф с заданным паросочетанием, Т – дерево достижимости для вершины а. Вершина x принадлежит дереву Т тогда и только тогда, когда в графе существует чередующийся путь, соединяющий вершины a и x.
Для построения дерева достижимости можно использовать слегка модифицированный поиск в ширину из вершины a. Отличие от стандартного поиска в ширину состоит в том, что для вершин из доли А (они находятся на четном расстоянии от вершины а) исследуются инцидентные им слабые ребра, а для вершин из доли В – сильные. Если в дереве появляется отличная от а свободная вершина b, это означает, что найден увеличивающий путь – это путь между а и b в дереве. Выполнив инверсию, получим большее паросочетание. После этого, если в доле А еще имеются свободные вершины, возобновляется поиск увеличивающего пути (т.е. строится новое дерево достижимости).
Если дерево построено и в нем нет других свободных вершин, кроме корня, то нужно выбрать другую свободную вершину в доле А (если такие еще есть) и строить дерево достижимости для нее. Если деревья достижимости для всех свободных вершин из А построены, а увеличивающий путь не найден, то имеющееся паросочетание является наибольшим.
Допустим, дерево достижимости для вершины а построено и выяснилось, что нет увеличивающих путей, начинающихся в а. Затем было построено дерево достижимости с другим корнем, найден увеличивающий путь и построено увеличенное паросочетание. Нужно ли строить дерево достижимости для вершины а относительно нового паросочетания? Оказывается, нет. Назовем свободную вершину бесполезной для данного паросочетания, если нет увеличивающих путей, начинающихся в этой вершине. Пусть 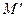 – паросочетание, полученное из паросочетания М инверсией относительно некоторого увеличивающего пути.
– паросочетание, полученное из паросочетания М инверсией относительно некоторого увеличивающего пути.
Утверждение. Если вершина а бесполезна для паросочетания М, то она бесполезна и для паросочетания 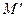 .
.
Таким образом, каждая вершина может выступать в качестве корня дерева достижимости не более одного раза, т.е. всего будет построено не более n деревьев. Построение одного дерева выполняется за время 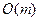 и общее время работы алгоритма оценивается как
и общее время работы алгоритма оценивается как 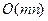 .
.
 2014-02-04
2014-02-04 1567
1567








