Описанный метод построения наибольшего паросочетания называют методом чередующихся путей. Он может применяться и для решения других задач. Рассмотрим задачу о независимом множестве. Она трудна в общем случае, но для двудольных графов допускает достаточно быстрое решение с помощью метода чередующихся путей.
Пусть 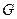 – двудольный граф с долями А и В и требуется найти в нем наибольшее независимое множество. Найдем сначала наибольшее паросочетание М в этом графе. Пусть
– двудольный граф с долями А и В и требуется найти в нем наибольшее независимое множество. Найдем сначала наибольшее паросочетание М в этом графе. Пусть 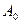 и
и 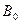 соответственно множества свободных вершин в долях А и В. Найдем все вершины из А, достижимые чередующимися путями из
соответственно множества свободных вершин в долях А и В. Найдем все вершины из А, достижимые чередующимися путями из 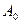 , пусть
, пусть 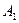 – множество всех таких вершин. Аналогично, пусть
– множество всех таких вершин. Аналогично, пусть 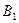 – множество все вершин из В, достижимых чередующимися путями из
– множество все вершин из В, достижимых чередующимися путями из 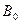 . Обозначим через
. Обозначим через 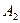 множество всех вершин из А, не достижимых чередующимися путями ни из
множество всех вершин из А, не достижимых чередующимися путями ни из 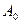 , ни из
, ни из 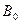 (см. рисунок 10). Вершины из
(см. рисунок 10). Вершины из 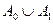 не смежны с вершинами из
не смежны с вершинами из 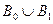 , так как иначе образовался бы увеличивающий путь. Вершины из
, так как иначе образовался бы увеличивающий путь. Вершины из 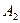 тоже не смежны с вершинами из
тоже не смежны с вершинами из 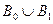 , иначе они были бы достижимы из
, иначе они были бы достижимы из 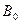 . Значит,
. Значит, 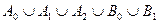 – независимое множество. Оно содержит все свободные вершины и по одной вершине из каждого ребра паросочетания. Отсюда следует, что это независимое множество – наибольшее. Паросочетание М состоит из
– независимое множество. Оно содержит все свободные вершины и по одной вершине из каждого ребра паросочетания. Отсюда следует, что это независимое множество – наибольшее. Паросочетание М состоит из 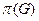 ребер, а свободных вершин имеется ровно
ребер, а свободных вершин имеется ровно 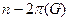 . Следовательно,
. Следовательно, 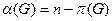 . Так как
. Так как 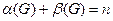 , то справедливо следующее утверждение.
, то справедливо следующее утверждение.
|
|
|
Теорема о числе вершинного покрытия двудольного графа. Для любого двудольного графа G выполняется равенство 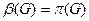 .
.

Рис. 10.
 2014-02-04
2014-02-04 1129
1129








