2014-02-04
1068
Вернемся к задаче вариационного исчисления, т.е. среди всех близких кривых 
найдём такую функцию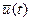 
, при которой выполняется условие (4.2).
Предположим, что функция, при которой выполняется условие (4.2), известна. Обозначим её 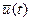. Пусть начала и концы оптимальной 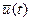и неоптимальной кривых совпадают (см. рис. 4.2). Для кривых близких в смысле первого порядка кривые отличаются только крутизной наклона, т.е. первыми производными. Тогда для неоптимальной кривой можно записать, что
,
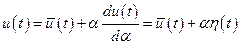где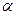 
– малое число;
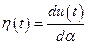– произвольная гладкая функция, которая в начальный и конечный моменты времени равна нулю 
;
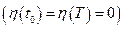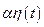– называется вариацией функции .
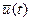С учётом этого функционал (4.1) можно записать в виде:
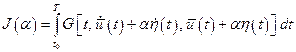. (4.3)
Необходимое условие оптимальности (экстремальности) функции 
– равенство нулю первой производной по переменной 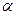. Найдём 
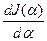и приравняем к нулю.
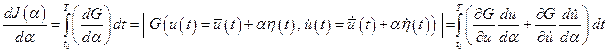. (4.3)`
С учетом того, что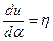 
; 
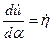выражение (4.3)` можно представить в виде:
.
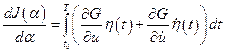Рассмотрим второе слагаемое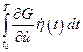 
.
Используем свойство интегралов
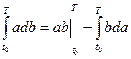. (4.4)
Обозначим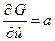 
, тогда 
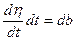. Найдём 
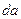и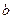 
в (4.4). Для этого продифференцируем 
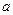по времени 
: 
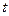. Откуда следует, что 
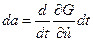. Так как 
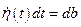, то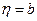 
.
Тогда второе слагаемое можно записать следующим образом:
.
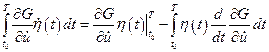Множитель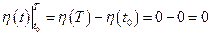 
по условию.
Тогда
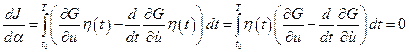. (4.5)
Воспользуемся леммой Лагранжа: если для каждой непрерывной функци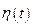и 
и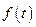 
интеграл 
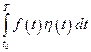тождественно равен нулю при всех 
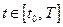, то либо 
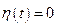, либо 
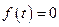. По условию мы приняли, что 
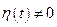. Тогда 
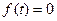. С учётом этого можно записать, что
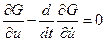. (4.6)
Полученное уравнение (4.6) называется уравнением Эйлера.
Так как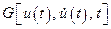 
, то
.
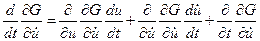Тогда уравнение Эйлера в развернутой форме примет вид:
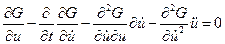. (4.7)
Таким образом, решив уравнение Эйлера (дифференциальное уравнение второго порядка) с использованием двух граничных условий, можно найти оптимальное управление 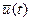, при котором 
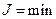. Такая функция 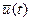называется экстремалью.
