Непрерывно-детерминированные модели (Д-схемы)

Если в модели системы не учитывается воздействие случайных факторов, а операторы переходов и выходов непрерывны (это означает, что малые изменения входных воздействий приводят к такого же порядка малым изменениям выходного воздействия и состояния системы), то состояния системы и выхода соответственно могут быть представлены в виде дифференциальных уравнений:

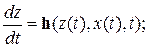(3.6)

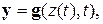(3.7)

где h, g – вектор-функции состояний и выходов соответственно; х, z, у – векторы входных воздействий, состояний и выходных воздействий соответственно.

Дифференциальными уравнениями называются такие уравнения, в которых неизвестными будут функции одной переменной или нескольких переменных, причём в уравнение входят не только их функции, но их производные различных порядков. Если неизвестные – функции многих переменных, то уравнения называются – уравнения в частных производных. Если неизвестные функции одной независимой переменной, то имеют место обыкновенные дифференциальные уравнения.

Математическое соотношение для детерминированных систем в общем виде:

.

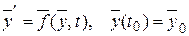В случае линейности таких систем, когда операторы переходов и выходов обладают свойствами однородности и аддитивности, вид уравнений (3.6) и (3.7) упрощается, что дает возможность аналитического решения или исследования известными методами с помощью вычислительных машин.

Построение математических моделей непрерывных линейных детерминированных систем в виде дифференциальных уравнений используется при анализе функционирования элементов и электрических цепей приборных систем.

3.3. Дискретно-детерминированные модели (F -схемы)

Дискретно-детерминированные модели (ДДМ) являются предметом рассмотрения теории автоматов (ТА) – раздела теоретической кибернетики, изучающей устройства, перерабатывающие дискретную информацию и меняющие свои внутренние состояния лишь в допустимые моменты времени.

Конечный автомат (КА) имеет множество внутренних состояний и входных сигналов, являющихся конечными множествами. Автомат задаётся F -схемой:

F = < z, x, y, j, y, z ₀>, (3.8)

где z, x, y – соответственно конечные множества входных, выходных сигналов (алфавитов) и конечное множество внутренних состояний (алфавита). z ₀ Î Z – начальное состояние; j(z, x) – функция переходов; y(z, x) – функция выхода. Автомат функционирует в дискретном автоматном времени, моментами которого являются такты, т.е. примыкающие друг к другу равные интервалы времени, каждому из которых соответствуют постоянные значения входного, выходного сигнала и внутреннего состояния. Абстрактный автомат имеет один входной и один выходной каналы.

В момент t, будучи в состоянии z (t), автомат способен воспринять сигнал x (t) и выдать сигнал y (t) = y[ z (t), x (t)], переходя в состояние z (t + 1) = j[ z (t), z (t)], z (t) Î Z; y (t) Î Y; x (t) Î X. Абстрактный КА в начальном состоянии z ₀, принимая сигналы x (0), x (1), x (2), … (входное слово), выдаёт сигналы y (0), y (1), y (2), … (выходное слово).

Существуют:

1) F -автомат 1-ого рода (автомат Миля), функционирующий по схеме:

z (t + 1) = j[ z (t), z (t)], t = 0, 1, 2, … (3.9)

y (t) = y[ z (t), x (t)], t = 0, 1, 2, …; (3.10)

2) F -автомат 2-ого рода:

z (t + 1) = j[ z (t), z (t)], t = 0, 1, 2, … (3.11)

y (t) = y[ z (t), x (t – 1)], t = 1, 2, 3, …; (3.12)

2) F -автомат 2-ого рода, для которого функция выходов не зависит от входной переменной x (t) (автомат Мура):

z (t + 1) = j[ z (t), z (t)], t = 0, 1, 2, … (3.13)

y (t) = y[ z (t)], t = 0, 1, 2, …; (3.14)

Таким образом, уравнения (3.9-3.14), полностью задающие F -автомат, являются частным случаем уравнения:

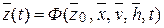, (3.15)

где 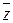– вектор состояний, 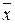– вектор независимых входных переменных, 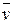– вектор воздействий внешней среды, 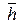– вектор собственных внутренних параметров системы, 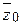– вектор начального состояния, t – время; и уравнения

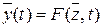, (3.16)

когда система S – денорминированная, и на её вход поступает дискретный сигнал x.

По числу состояний конечные автоматы бывают с памятью и без памяти. Автоматы с памятью имеют более одного состояния, а автоматы без памяти (комбинационные или логические схемы) обладают лишь одним состоянием. При этом согласно (3.10) работа комбинационной схемы заключается в том, что она ставит в соответствие каждому входному сигналу x (t) определённый выходной сигнал y (t), т.е. реализует логическую функцию вида:

y (t) = y[ x (t)], t = 0, 1, 2, …

Эта функция называется булевой, если алфавиты X и Y, которым принадлежат значения сигналов x и y, состоят из 2-х букв.

По характеру отсчёта времени (дискретному) F -автоматы делятся на синхронные и асинхронные. В синхронных автоматах моменты времени, в которые автомат «считывает» входные сигналы, определяются принудительно синхронизирующими сигналами. Реакция автомата на каждое значение входного сигнала заканчивается за один такт синхронизации. Асинхронный F -автомат считывает входной сигнал непрерывно, и поэтому, реагируя на достаточно длинный водной сигнал постоянной величины x, он может, как это следует из 3.8-3.14, несколько раз изменить своё состояние, выдавая соответствующее число выходных сигналов, пока не перейдёт в устойчивое.

Для задания F -автомата необходимо описать все элементы множества F = < z, x, y, j, y, z ₀>, т.е. входной, внутренний и выходной алфавиты, а также функции переходов и выходов. Для задания работы F -автоматов наиболее часто используются табличный, графический и матричный способ.

В табличном способе задания используется таблицы переходов и выходов, строки которых соответствуют входным сигналам автомата, а столбцы – его состояниям. При этом обычно 1-ый столбец слева соответствует начальному состоянию z ₀. На пересечении i -ой строки и j -ого столбца таблицы переходов помещается соответствующее значение j(z_k, x_i) функции переходов, а в таблице выходов – y(z_k, x_i) функции выходов. Для F -автомата Мура обе таблицы можно совместить, получив отмеченную таблицу переходов, в которой над каждым состоянием z_k автомата, обозначающим столбец таблицы, стоит соответствующий этому состоянию, согласно (3.14), выходной сигнал y(z_i).

Описание работы F -автомата Миля таблицами переходов j и выходов y иллюстрируется таблицей 3.1, а описание F -автомата Мура – таблицей переходов 3.2.

Таблица 3.1	Таблица 3.2
xi zk z 0 z 1 … zk Переходы x 1 j(z 0, x 1) j(z 1, x 1) … j(zk, x 1) x 2 j(z 0, x 2) j(z 1, x 2) … j(zk, x 2) ………………………………………… xn j(z 0, xn) j(z 1, xn) … j(zk, xn) Выходы x 1 y(z 0, x 1) y(z 1, x 1) … y(zk, x 1) ………………………………………… xn y(z 0, xn) y(z 1, xn) … y(zk, xn)	xi y(zk) y(z 0) y(z 1) … y(zk) z 0 z 1 … zk x1 j(z 0, x 1) j(z 1, x 1) … j(zk, x 1) x2 j(z 0, x 2) j(z 1, x 2) … j(zk, x 2) ……………………………………… xn j(z 0, xn) j(z 1, xn) … j(zk, xn)

При другом способе задания конечного автомата используется понятие направленного графа. Граф автомата представляет собой набор вершин, соответствующих различным состояниям автомата и соединяющих вершин дуг графа, соответствующих тем или иным переходам автомата. Если входной сигнал x_k вызывает переход из состояния z_i в состояние z_j, то на графе автомата дуга, соединяющая вершину z_i с вершиной z_j, обозначается x_k. Для того чтобы задать функцию переходов, дуги графа необходимо отметить соответствующими выходными сигналами. Для автоматов Миля эта разметка производиться так: если входной сигнал x_k действует на состояние z_i, то получается дуга, исходящая из z_i и помеченная x_k; эту дугу дополнительно отмечают выходным сигналом y = y(z_i, x_k). Для автомата Мура аналогичная разметка графа такова: если входной сигнал x_k, действуя на некоторое состояние автомата, вызывает переход в состояние z_j, то дугу, направленную в z_j и помеченную x_k, дополнительно отмечают выходным сигналом y = y(z_j, x_k). На рис. 3.1 приведены заданные ранее таблицами F -автоматы Миля F ₁ и Мура F ₂ соответственно.

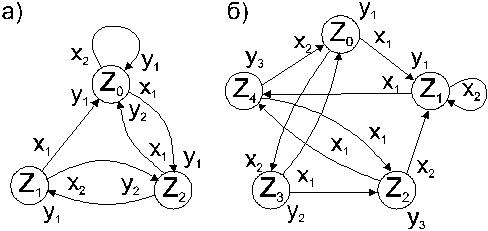
Рис. 3.1. Графы автоматов Миля (а) и Мура (б)

При решении задач моделирования часто более удобной формой является матричное задание конечного автомата. При этом матрица соединений автомата есть квадратная матрица 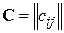, строки которой соответствуют исходным состояниям, а столбцы – состояниям перехода. Элемент c_ij = x_k / y_s в случае автомата Миля соответствует входному сигналу x_k, вызывающему переход из состояния z_i в состояние z_j, и выходному сигналу y_s, выдаваемому при этом переходе. Для автомата Миля F ₁, рассмотренного выше, матрица соединений имеет вид:

.

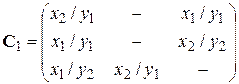Если переход из состояния z_i в состояние z_j происходит под действием нескольких сигналов, элемент матрицы c_ij представляет собой множество пар «вход/выход» для этого перехода, соединённых знаком дизъюнкции.

Для F -автомата Мура элемент c_ij равен множеству входных сигналов на переходе (z_i ® z_j), а выход описывается вектором выходов:

,

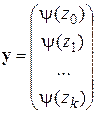i -ая компонента которого выходной сигнал, отмечающий состояние z_i.

Для детерминированных автоматов переходы однозначны. Это означает, что в графе F -автомата из любой вершины не могут выходить 2 и более ребра, отмеченные одним и тем же входным сигналом. Аналогично этому в матрице соединений автомата C в каждой строке любой входной сигнал не должен встречаться более одного раза.

Для F -автомата состояние z_k называется устойчивым, если для любого входа x_i Î X, для которого j(z_k, x_i) = z_k имеет место y(z_k, x_i) = y_k. Таким образом, F -автомат называется асинхронным, если каждое его состояние z_k Î Z устойчиво.

На практике всегда автоматы являются асинхронными, а устойчивость их состояний обеспечивается тем или иным способом, например, введением сигналов синхронизации. На уровне абстрактной теории удобно оперировать синхронными конечными автоматами.

Если в таблице переходов асинхронного автомата некоторое состояние z_k стоит на пересечении строки x_s и столбца z_s (s ¹ k), то это состояние z_k обязательно должно встретиться в этой же строке в столбце z_k.

С помощью F -схем описываются узлы и элементы ЭВМ, устройства контроля, регулирования и управления, системы временной и пространственной коммутации в технике обмена информацией. Широта применения F -схем не означает их универсальность. Этот подход непригоден для описания процессов принятия решений, процессов в динамических системах с наличием переходных процессов и стохастических элементов.

4. Непрерывно-стохастические модели (Q -схемы)

К ним относятся системы массового обслуживания (queuing systems), которые называют Q -схемами.

Теория массового обслуживания составляет один из разделов теории вероятностей. В этой теории рассматриваются вероятностные задачи и математические модели.

Детерминированная математическая модель отражает поведение объекта (системы, процесса) с позиций полной определенности в настоящем и будущем. Вероятностная математическая модель учитывает влияние случайных факторов на поведение объекта (системы, процесса) и, следовательно, оценивает будущее с позиций вероятности тех или иных событий, т.е. задачи рассматриваются в условиях неопределенности.