Разыгрывание непрерывной случайной величины
Пусть требуется разыграть непрерывную случайную величину Х, т.е. получить последовательность ее возможных значений xi (i = 1, 2, …). При этом функция распределения F (X) известна.
Существует следующая теорема.
Если ri – случайное число, то возможное значение xi разыгрываемой непрерывной случайной величины Х с известной функцией распределения F (X), соответствующее ri, является корнем уравнения F (xi) = ri.
Алгоритм разыгрывания непрерывной случайной величины:
1. Необходимо выбрать случайное число ri.
2. Приравнять выбранное случайное число известной функции распределения F (X) и получить уравнение F (xi) = ri.
3. Решить данное уравнение относительно xi. Полученное значение xi будет соответствовать одновременно и случайному числу ri, и заданному закону распределения F (X).
Известно, что если случайная величина R распределена равномерно в интервале (0, 1), то ее математическое ожидание М (R) = 1/2, а дисперсия D (R) =1/12.
Составим сумму n независимых случайных величин Rj (j = 1, 2, …, n), которые распределены равномерно в интервале (0, 1). Получим 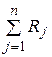 .
.
|
|
|
Пронормируем эту сумму. Для этого найдем сначала ее математическое ожидание и дисперсию. Известно, что математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых. Сумма Rj содержит n слагаемых. Математическое ожидание каждого слагаемого равно 1/2. Следовательно, математическое ожидание суммы равно:
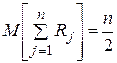 .
.
Аналогично для дисперсии суммы Rj получим:
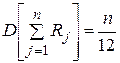 .
.
Отсюда среднее квадратическое отклонение суммы Rj:
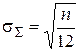 .
.
Теперь пронормируем сумму Rj.
Для этого вычтем из суммы Rj математическое ожидание этой суммы и разделим на среднее квадратическое отклонение суммы Rj. Получим:
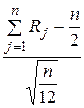 , то есть
, то есть 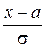 .
.
На основании центральной предельной теоремы теории вероятностей при n ® ¥ распределение этой нормированной случайной величины стремится к нормальному закону с параметрами a = 0 и s = 1.
Если требуется разыграть значения нормальной ненормированной случайной величины с математическим ожиданием a отличным от нуля и s отличным от единицы, то сначала разыгрывают возможные значения xi нормированной случайной величины, а затем находят искомое значение по формуле  , которая получена из соотношения
, которая получена из соотношения 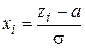 .
.
Таблица 8.1
Формулы для моделирования случайных величин
| Закон распределения случайной величины | Плотность распределения | Формула для моделирования случайной величины |
| Экспоненциальный | 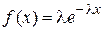
| 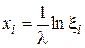
|
| Вейбула | 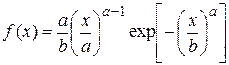
| 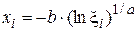
|
| Гамма-распределение (h – целые числа) | 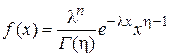
| 
|
| Нормальное | 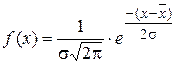
| 
|
 2014-02-04
2014-02-04 1688
1688








