Метод сечений

Пусть в пространстве дана прямоугольная система координат 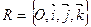и поверхность S. Будем пересекать поверхность плоскостями s ₁, s ₂, …, s_n, параллельными координатным плоскостям xOy, xOz, yOz. Тем самым найдем линии пересечения плоскости s_i с поверхностью S. По виду линий вынесем суждение о форме поверхности S.

Применение метода сечений основано на теореме:

Теорема 17.1

В ортонормированном репере заданы поверхность S: F(x; y; z)=0 и плоскость s: z=h, параллельная хОу или совпадающая с ней. Если поверхность S пересекает плоскость s по линии g, то проекция g ¢ линии g на плоскость хОу имеет уравнение

F (x; y; h)=0 (17..3), где h =0.

Дано: 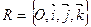, поверхность S: F (x; y; z)=0, плоскость s: z=h,

S Ç s = g, g ¢=пр _хОуg.

Доказать: g: F (x; y; h)=0.

Доказательство. Покажем, что точка проекции g ¢ удовлетворяет уравнению (17.3), а никакая другая точка не удовлетворяет ему.

Пусть точка М ¢(х ¢; у ¢; 0)Î g ¢. Тогда для точки М ¢ существует прообраз – точка плоскости s М Î g, причем М (х ¢; у ¢; h).

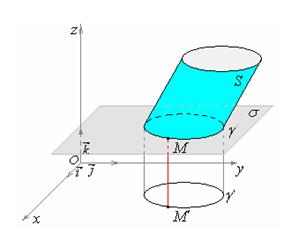
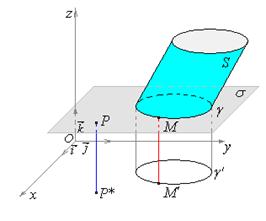
По условию gÌS, т.е. М Î S, значит, ее координаты удовлетворяют уравнению S: F (x ¢; y ¢; h)=0.

Пусть точка Р* (х *; у *; 0)Ï g ¢. Тогда для точки Р* существует прообраз – точка Р Î s, тогда Р * – проекция точки Р (х *; у *; h). Р* Ï g ¢, следовательно, Р Ï g, следовательно, Р Ï S, значит, ее координаты не удовлетворяют уравнению S: F (x ¢; y ¢; h)¹0.

Следствие.

Линия g пересечения поверхности S с плоскостью s, параллельной координатной плоскости хОу, равна проекции g ¢ этой линии на плоскость хОу.