Формула Пуазейля. Единицей вязкости в СИ является такая вязкость, при которой градиент скорости, равный 1 м/сек на 1 м

Единицей вязкости в СИ является такая вязкость, при которой градиент скорости, равный 1 м/сек на 1 м, приводит к возникновению силы внутреннего трения в 1 Н на 1 м2 поверхности касания слоев.

При движении жидкости в круглой трубе скорость равна нулю у стенок трубы, максимальна на оси трубы и, как можно показать, при не слишком больших скоростях течения изменяется вдоль любого радиуса по закону

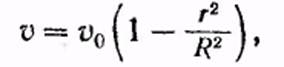(7.11)

скорость на расстоянии r от оси трубы (рис. 7.6). Проведем в жидкости мысленно цилиндрическую поверх­ность радиуса r.

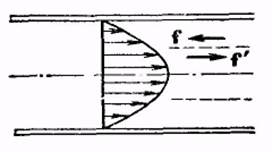рис. 7.6

Части жидкости, лежащие по разные стороны от этой поверхности, действуют друг на друга, с силой, величина которой в расчете на единицу поверхно­сти равна 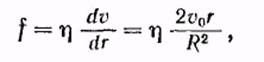(7.12) т. е. возрастает пропорционально расстоянию поверхности раздела от оси трубы.

Пусть вязкая несжимаемая жидкость течет вдоль прямолинейной цилиндрической трубы радиуса R. Линии тока параллельны оси трубы. Если выделить произвольную бесконечно узкую трубку тока, то из условия несжимаемости следует, что скорость течения v будет одна и та же вдоль всей трубки тока — скорость жидкости не может меняться вдоль трубы. Но она, конечно, может изменяться с изменением расстояния r от оси трубы. Таким образом, скорость жидкости v является функцией радиуса r.

Примем ось трубы за ось X, направленную в сторону тече­ния. Выделим в трубе произвольную бесконечно короткую цилиндрическую часть длины dx и радиуса. На ее боковую поверхность в направлении движения действует касательная сила внутреннего трения

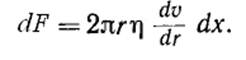
Кроме того, на основания цилиндра в том же направлении действует сила разности давлений dF

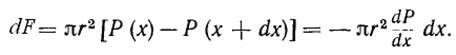
При стационарном течении сумма этих двух сил должна обращаться в нуль, а потому

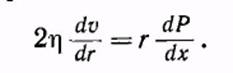
Скорость v (r), а с ней и производная 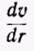не меняются с изменением х.

Поэтому должна быть постоянной и производная 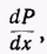причем эта производная должна быть равна 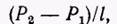где P₁ — давление на входе трубы, Р₂ — на выходе, а l — длина трубы. В результате приходим к уравнению

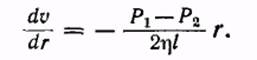
Интегрируя, получим

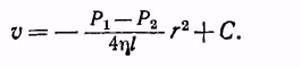
Постоянная интегрирования С определится из условия, что на стенке трубы, т. е. при r = R скорость v должна обращаться в нуль. Это дает

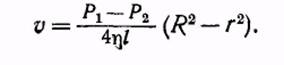(7.13)

Скорость v максимальна на оси трубы, где она достигает значения

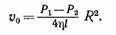(7.14)

При удалении от оси скорость v меняется по параболическому закону.

Определим расход жидкости, т. е. количество ее, ежесе­кундно протекающее через поперечное сечение трубы. Масса жидкости, ежесекундно протекающая через кольцевую площадку с внутренним радиусом r и внешним r + dr, равна 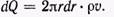Подставляя сюда выражение для v (7.13)и интегрируя, находим искомый расход жидкости

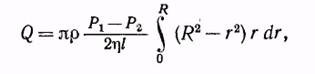
Или

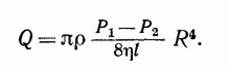(7.15)

Расход жидкости пропорционален разности давлений P_t — Р₂, четвертой степени радиуса трубы и обратно пропорционален длине трубы и коэффициенту вязкости жидкости. Формула (7.15) называется формулой Пуазейля, хотя сам Пуазейль и не выводил ее, он исследовал вопрос только экспериментально. На формуле Пуазейля основан один из экспериментальных методов определения коэффициентов вязкости жидкостей.