Теория матричных игр

В 3-й главе уже упоминались матричные игры – один из наиболее важных типов антагонистических игр. Теория матричных игр разработана более подробно по сравнению с общей теорией антагонистических игр. Известны различные алгоритмы поиска оптимальных стратегий игроков в матричной игре, они в большинстве своём наглядны и просты в применении, выбор алгоритма зачастую определяется размерностью матрицы.

Рассмотрим примеры поиска седловой точки в матричной игре. Поиск проводится так: проверяется истинность соотношения минимакса, если оно

выполняется, то седловые точки – это все пары стратегий 1-го и 2-го игроков

(каждой паре соответствуют номер строки и номер столбца), выигрыш при которых равен цене игры, а также минимален среди выигрышей - элементов

строки и максимален среди выигрышей - элементов столбца. Если же соотношение минимакса не выполнено, то седловых точек нет.

Пример 4.1.

min a

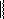
j ij

⎛1

⎜

A = ⎜0

−3 − 2 ⎞

⎟

5 4 ⎟

−3⎫

⎪

⎬

max min aij = 2

⎜ ⎟ ⎪ i j

⎝ ⎠ ⎭

max aij = 2 5 4 4

i 1423

min max aij = 2

j i

Седловой точкой является пара (3,1), при которой υ= v = v = 2.

Заметим, что хотя выигрыш в точке (3,3) также равен 2 = v = v, она не

является седловой точкой, т.к. этот выигрыш не является максимальным среди выигрышей третьего столбца.

Пример4.2.

min a

⎛10

A = ⎜

30 ⎞

⎟

j ij

→

10 ⎫

⎬max min aij

= 20

⎝40 max aij ↓

20 ⎠ →

↓

20⎭ i j

40 30

min max a

=30

j i ij

Из матрицы выигрышей видно, что

v < v, т.е. данная матрица не имеет

седловой точки. Если игрок 1 выбирает свою максиминную (ту, что гарантирует ему выигрыш в размере нижней цены игры) стратегию i = 2, то игрок 2, выбрав свою минимаксную (ту, что гарантирует ему проигрыш в размере не большем, чем верхняя цены игры) стратегию j = 2, проиграет только 20. В этом случае игроку 1 выгодно выбрать стратегию i = 1, т.е. отклониться от своей максиминной стратегии и выиграть 30. Тогда игроку 2 будет выгодно выбрать стратегию j = 1, т.е. отклониться от своей минимаксной стратегии и проиграть 10. В свою очередь игрок 1 должен выбрать свою 2-ю стратегию, чтобы выиграть 40, а игрок 2 ответит выбором

2-й стратегии.

Пример 4.3.

Рассмотрим игровую матрицу, в которой один из элементов (а именно, a 33) неизвестен. Обозначим этот элемент x. Установим, при каких значениях x в матрице есть седловые точки.

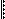min a

j ij

⎛1 5 4 ⎞

⎜ ⎟

A= ⎜3 2 0 ⎟

1 ⎫

⎪

⎭

0 ⎬maxmin aij

= max[1,min{5, x }].

max aij =

⎜ ⎟

⎝ ⎠

3 6 max(4, x)

min{5, x }⎪ i j

i 144424443

minmax aij = 3

j i

Таким образом, матрица имеет седловую точку при x =3. Это точка (3,3). Других седловых точек в матрице нет. Выигрыш в точке (2,1) также равен 3, но она не является седловой точкой, т.к. этот выигрыш не является максимальным среди выигрышей первого столбца.

Можно легко найти и другие матрицы, не имеющие седловых точек (в частности, из примеров 3.1 и 3.2). Более того, можно утверждать, что и в реальной ситуации матрица, которой задается игра, чаще всего не имеет

седловых точек. Таким образом, игроки не имеют оптимальных стратегий,

им нужно искать новые критерии выбора.

Первый игрок всегда может обеспечить себе выигрыш

υ = max

min

aij, а второй - выигрыш υ =

min

max

aij,

но в

1 ≤ i ≤ n 1 ≤

j ≤ m

1 ≤ j ≤ m 1 ≤ i ≤ n

общем случае υ <υ

и, следовательно, создается неустойчивая ситуация,

которую один из игроков может изменить с выгодой для себя. Значит, игрокам следует искать дополнительные стратегические возможности для того, чтобы гарантировать себе больший выигрыш и меньший проигрыш соответственно. Можно более широко понимать стратегию как объект: не только как действие, но в общем случае еще и как правило, по которому выбирается действие. Таким образом, выбор игроков значительно расширяется. Один из возможных путей - выбирать свои стратегии случайно, то есть задать распределение вероятностей на множестве своих стратегий, а после этого предоставить выбор конкретной стратегии соответствующему случайному механизму.

Итак, выбор игроком своей стратегии с заранее заданной вероятностью является одним из способов действия, то есть в определенном смысле тоже

стратегией. Для отличия стратегий такого вида от первоначально заданных стратегий их называют смешанными стратегиями, а первоначально заданные (то есть строки или столбцы матрицы) - чистыми стратегиями. Переход к

смешанным стратегиям позволяет получить большинство важных результатов, относящихся к матричным играм. Более того, можно сказать, что только этот переход позволяет полностью решить игру.

Определение. Смешанной стратегией игрока 1 в матричной игре называется распределение вероятностей на множестве его чистых стратегий,

то есть любой вектор x = (x 1,..., xn), обладающий свойствами:

xi ≥ 0, i =1,..., n;

(4.1)

∑ xi

i =1

=1.

(4.2)

Смешанной стратегией игрока 2 в матричной игре называется распределение вероятностей на множестве его чистых стратегий, то есть любой вектор

y = (y 1,..., yn),

обладающий свойствами

yj ≥ 0,

j =1,..., m;

(4.3)

∑ yj

j =1

=1.

(4.4)

Число

xi, i =1,..., n,

представляет собой вероятность выбора i -й чистой

стратегии игроком 1, а

yj,

j =1,..., m

- вероятность выбора j -й чистой

стратегии игроком 2. i -й чистой стратегии игрока 1 соответствует смешанная стратегия

ei = (0,...,1,...,0),

(4.5)

а j -й чистой стратегии игрока 2 - смешанная стратегия

fj = (0,...,1,...,0).

(4.6)

Таким образом, множество смешанных стратегий бесконечно. Применение смешанных стратегий превращает процесс игры в некоторое случайное испытание, исходами которого являются ситуации игры, то есть пары (i, j). Это случайное испытание называется ситуацией в смешанных

стратегиях и обозначается через

(x, y).

Отсутствие обмена информацией

между игроками в антагонистической игре делает случайные принятия ими решения о своих стратегиях i и j независимыми. Поэтому каждая ситуация (i, j) реализуется с вероятностью хiyj. Поскольку в этой ситуации игрок 1 получает выигрыш aij, математическое ожидание его выигрыша равно

n m

F (x, y) = ∑∑ aijxiyj.

i =1 j =1

(4.7)

Определение. Матричной игрой (со смешанными стратегиями) называется тройка Г= (Х, Y, F), где Х - множество векторов, удовлетворяющих условиям (4.1), (4.2), Y - множество векторов, удовлетворяющих условиям (4.3), (4.4), F (x, y) - функция, заданная

формулой (4.7).

В дальнейшем под матричной игрой понимается объект, заданный именно таким определением.

ТЕОРЕМА 4.1(основная теорема теории матричных игр). Любая матричная игра имеет седловую точку в смешанных стратегиях.

Доказательство. Покажем, что в данном случае выполнены все условия теоремы 3.4.

Ограниченность Х и Y вытекает из условий (4.1)-(4.4). Докажем замкнутость и выпуклость этих множеств. Доказательство проведем для Х, для Y оно аналогично.

Покажем замкнутость Х. Пусть

′

xk ∈ X

при всех k,

x ′ =

lim

k → ∞

x k.

Докажем, что и

x ∈ X.

В самом деле,

k ≥ 0

при всех k и i =1,…, n,

следовательно,

lim xk

k → ∞ i

≥ 0 при всех i =1,…, n, то есть

x ′ ≥ 0

при всех

i =1,…, n. Далее, поскольку

∑ xk

i =1 i

=1 при всех k, то и

lim ∑ x k

k → ∞ i =1 i

=1, то

есть

∑

i =1

x ′ =1. Таким образом,

′

x ∈ X

удовлетворяет условиям (4.1), (4.2)

и принадлежит Х. Итак, Х является замкнутым.

Покажем выпуклость Х. Пусть x 1 ∈ X,

x 2 ∈ X и 0 ≤ λ≤1.

Так как

∀ i =1,..., n

x 1 ≥ 0,

x 2 ≥ 0,

получаем: ∀ i =1,..., n λ x 1 + (1− λ) x 2 ≥ 0.

i i i i

n n

А условия

∑

i =1

x 1 =1 и

∑

i =1

=1 влекут за собой соотношение:

∑ (λ x 1 + (1− λ) x 2) =1.

i i

I =1

Следовательно, λ

x 1 + (1 − λ) x 2 обладает свойствами (4.1), (4.2) и

принадлежит Х. Таким образом, Х является выпуклым.

Непрерывность функции F (x, y), вогнутость по x и выпуклость по y

вытекает из ее линейности.

Таким образом, матричная игра Г= (Х, Y, F) удовлетворяет всем условиям теоремы 3.4.

Следовательно, в ней существует седловая точка, что и требовалось доказать.

ЛЕММА 4.1. Справедливы равенства

F (ei, y) =

∑

j =1

aij yj;

(4.8)

F (x, fj) =

∑

i =1

aij xi;

(4.9)

F (x, y) =

∑

i =1

xi F (ei, y) =

∑

j =1

y j F (x, f j).

(4.10)

Утверждение леммы вытекает непосредственно из соотношений (4.7), (4.5) и (4.6).

Замечание.

Если

равенства

x 0, y 0

- оптимальные стратегии, υ- цена игры, то верны

min F (x 0, y) = max min F (x, y) =υ;

(4.11)

y x y

max F (x, y 0) = min max F (x, y) =υ;

(4.12)

x y x

F (x 0, y 0) =υ.

(4.13)

В следующей серии теорем (с номерами 4.2–4.7) выражены основные свойства оптимальных стратегий матричной игры.

ТЕОРЕМА 4.2. Пусть υ- цена игры. Для того, чтобы x 0

была

оптимальной стратегией игрока 1, необходимо и достаточно, чтобы выполнялось условие

∀ yF (x 0, y) ≥υ.

(4.14)

Для того, чтобы y 0

была оптимальной стратегией игрока 2, необходимо и

достаточно, чтобы выполнялось условие

Доказательство.

∀ xF (x, y 0) ≤υ.

(4.15)

Необходимость. Если x 0

и y 0 - оптимальные стратегии, то (x 0, y 0) –

седловая точка, т.е. справедливо соотношение (3.4), из которого с учетом

(4.13) вытекает выполнение условий (4.14) и (4.15).

Достаточность. Пусть υ- цена игры и при всех y

y ′) – седловая точка, т.е. верно условие

F (x 0, y) ≥υ.

Пусть (x ′,

∀ x, y

F (x, y ′) ≤ F (x ′, y ′) ≤ F (x ′, y).

(4.16)

Покажем, что (x 0, y ′) – также седловая точка. Из (4.14) и (4.16) имеем

F (x 0, y ′) ≥υ,

F (x 0, y ′) ≤ F (x ′, y ′) =υ.Тогда

F (x 0, y ′) =υ. Но тогда из (4.14)

вытекает соотношение ∀ y

F (x 0, y) ≥ F (x 0, y ′), а из (4.16) – соотношение

∀ xF (x, y ′) ≤ F (x 0, y ′). Эти соотношения в совокупности означают, что (x 0,

y ′) – седловая точка и, следовательно, x 0

- оптимальная стратегия первого

игрока. То, что аналогично.

y 0 - оптимальная стратегия второго игрока, доказывается

ТЕОРЕМА 4.3. Множество оптимальных стратегий каждого игрока ограничено, замкнуто и выпукло.

Доказательство. Пусть Х 0 – множество оптимальных стратегий игрока 1, Y 0 –множество оптимальных стратегий игрока 2. Доказательство проведем для Х 0.

Ограниченность Х 0 вытекает из ограниченности множества Х и

включения Х 0⊂ Х.

Для доказательства замкнутости Х 0 достаточно показать, что для любой

последовательности стратегий на Х 0 предел этой последовательности также

содержится в Х 0. Пусть

xk ∈ X

при всех k,

lim xk

k → ∞

= x 0.

По теореме

4.2

F (xk, y) ≥υпри всех k и у. Переходя в этом неравенстве к пределу при

k → ∞, с учетом непрерывности F (x, y)получаем справедливость для x 0

соотношения (4.14). Таким образом, данная стратегия оптимальна.

Докажем выпуклость Х 0. Пусть

x 1 и

x 2 принадлежат Х, то есть

выполнены условия:

∀ y F (x 1, y) ≥υ, ∀ y

F (x 2, y) ≥υ.

Но тогда для

любого

0 ≤ λ≤1

и произвольного y имеем

F (λ x 1 + (1− λ) x 2) = λ F (x 1, y) + (1− λ) F (x 2, y) ≥υ. Таким образом,

λ x 1 + (1− λ) x 2

удовлетворяет условию (4.14) и, следовательно,

принадлежит Х 0. Теорема полностью доказана.

ТЕОРЕМА 4.4. Пусть υ – цена игры. Для того, чтобы x 0

была

оптимальной стратегией игрока 1, необходимо и достаточно, чтобы выполнялось условие

∀ j =1,..., m

F (x 0, fj) ≥υ.

(4.17)

Для того, чтобы y 0

была оптимальной стратегией игрока 2, необходимо и

достаточно, чтобы выполнялось условие

∀ i =1,..., n

F (ei, y 0) ≤υ.

(4.18)

Доказательство. Необходимость условий (4.17) и (4.18) вытекает непосредственно из теоремы 4.2. Доказательство достаточности проведем

для

x 0. Пусть для x 0

справедливо (4.17). Используя (4.10) и (4.17), для

любого y имеем:

F (x 0, y) =

∑

j =1

yjF (x 0, fj) ≥

∑

j =1

yj υ=υ.

Таким образом,

для x 0

справедливо условие (4.14) и, следовательно,

x 0 будет оптимальной

для первого игрока.

ТЕОРЕМА 4.5.

Для любого фиксированного y справедливо равенство

max F (x, y) =

max

1 ≤ i ≤ n

F (ei, y).

(4.19)

Для любого фиксированного x справедливо равенство

min F (x, y) =

min

F (x, f j).

(4.20)

y 1 ≤

j ≤ m

Таким образом, соответствующие максимумы и минимумы достигаются на чистых стратегиях.

Доказательство. Фиксируем некоторую стратегию x. Неравенство

min F (x, y) ≤

min

F (x,

fj) очевидно. Докажем противоположное

y 1 ≤

j ≤ m

неравенство. Для любого y имеем

∑ y k F (x, f k)	≥ min	F (x, f j	) ∑	y k =	min	F (x, f j).
k =1	1 ≤ j ≤ m		k =1		1≤ j ≤ m

F (x, y) =

Следовательно,

min F (x, y) ≥

min

F (x, fj)

и равенство (4.20) доказано.

y 1 ≤

j ≤ m

Равенство (4.19) доказывается аналогично.

Следствие. Если

верны соотношения

x 0, y 0

- оптимальные стратегии, υ– цена игры, то

min

F (x 0, f j) = m a x

min

F (x, f j) = υ;

(4.21)

1≤ j ≤ m

x 1≤

j ≤ m

max

1 ≤ i ≤ n

F (ei, y 0) = min

max

1 ≤ i ≤ n

F (ei, y) =υ.

(4.22)

ТЕОРЕМА 4.6. Пусть (x 0, y 0) – седловая точка. Тогда, если для

некоторого i

x 0 i ≠ 0, то

F (ei, y 0) =υ.

Аналогично, если для некоторого j

y 0 j

≠ 0, то

F (x 0, fj)=υ. Таким образом, в x 0

с положительной

вероятностью входят только те чистые стратегии, которые дают результат υ

против y 0 и в

y 0 с положительной вероятностью входят только те чистые

стратегии, которые дают результат υпротив

x 0.

Доказательство. Из (4.18) вытекает, что если

F (ei

, y 0) ≠υ

для

некоторого i, то

F (ei

, y 0) <υ. Покажем, что неравенство

F (ei, y 0) <υ

влечет за собой равенство

x 0 i = 0. В самом деле, если

x 0 i ≠ 0, то имеем

n n

υ = F (x 0, y 0) = ∑ x 0 i F (ei, y 0) < ∑ x 0 i υ =υ.

i =1

Пришли к противоречию, доказывающему утверждение теоремы

относительно

x 0. Для y 0

доказательство аналогично.

Определение. Вектор a называется выпуклой комбинацией векторов

a 1,..., a l, если существуют такие числа

λ1,...,λ l, что λ k

≥ 0при всех k =1,…, l.

l l

∑ λ k

k =1

=1 и

a = ∑ λ k ak.

k =1

Определение. Будем говорить, что вектор

a = (a 1,..., ap)доминирует

вектор

b = (b 1,..., bp), если

ak ≥ bk при всех k =1,…, p. Будем говорить, что

вектор

a = (a 1,..., a p)

строго доминирует вектор

b = (b 1,..., bp), если

ak > bk

при всех k =1,…, p.

ТЕОРЕМА 4.7. Если в матричной игре с матрицей А =(а ij), i =1,…, n; j =1,…, m i 0-я строка строго доминируется выпуклой комбинацией других строк, то i 0-я чистая стратегия игрока 2 не входит с положительной вероятностью ни в одну его оптимальную стратегию и, следовательно, при решении игры i 0-я строка может быть вычеркнута из матрицы. Если j 0-й столбец матрицы строго доминирует выпуклую комбинацию других столбцов, то j 0-я чистая стратегия игрока 2 не входит с положительной вероятностью ни в одну его оптимальную стратегию и, следовательно, при решении игры j 0-й столбец может быть вычеркнут из матрицы.

Доказательство. Пусть i 0-я строка матрицы строго доминируется

выпуклой комбинацией других строк, то есть существуют такие индексы

i 1,...,

ip и числа

λ i,...,λ i, что

ik ∈{1,..., n },

λ ik

≥ 0,

k =1,..., p,

∑ λ

k =1 k

=1 и

ai 0 j

< ∑

k =1

λ ikakj ∀ j =1,…, m. Положив

λ i = 0при i ∉{ i 1,..., ip },

мы можем

последнее условие представить так:

∀ j =1,..., m

ai j

< ∑

i =1

λ i aij. (4.23)

Вектор

(λ1,...,λ n)

удовлетворяет условиям: λ i

≥ 0,

i =1,..., n,

∑ λ i

i =1

=1,

то есть является смешанной стратегией игрока 1. Пусть y 0

- оптимальная

стратегия игрока 2. Исходя из (4.23), получим неравенства

F(ei 0, y 0 ) =

m m

∑ ai 0 jy 0 j < ∑

∑ y 0 j λ iaij

= F( λ ,y 0 ) ≤υ,

и по теореме 4.6

j = 1

j = 1 i = 1

выполняется

xi 0 = 0. Так как

y 0 - произвольная оптимальная стратегия

игрока 2,

ei 0

не входит ни в какую оптимальную стратегию игрока 1.

Утверждение о строго доминирующем столбце доказываем аналогично.

Следствие. Если i 0-я строка матрицы строго доминируется некоторой другой строкой, то при решении игры она может быть вычеркнута из матрицы. Если j 0-й столбец матрицы строго доминирует некоторый другой столбец, то при решении игры он может быть вычеркнут из матрицы.

Замечание. Если x

= (x 1,..., xi 0 −1, xi 0 +1,..., xn) - оптимальная стратегия

игрока 1 в игре, матрица которой образована вычеркиванием из начальной

матрицы i 0-й строки, то