2014-02-02
4010
В предыдущих главах мы исследовали антагонистические игры. Теперь рассмотрим общий случай игр двух игроков на конечных множествах стратегий с интересами, не являющимися противоположными (то есть неантагонистическими): у каждого игрока имеется своя функция выигрыша, не обязательно противоположная функции выигрыша противника.
Определение. Биматричной игрой называется система из четырех элементов Г= (Х, Y, F, G), где X ={1,…, n }, Y ={1,…, m }- конечные множества стратегий игроков 1 и 2 соответственно; F (i,j) и G (i,j) - их функции
выигрыша.
Функции выигрыша F и G можно задать матрицами А =(aij) и B =(bij) (i =1,…, n; j =1,…, m). Смешанные стратегии игроков и функции выигрыша для таких стратегий определяются так же, как и в матричных играх. Далее под биматричной игрой понимается игра со смешанными стратегиями.
Определение. Пара стратегий (x 0, y 0) называется ситуацией равновесия биматричной игры, если справедливы соотношения
∀ x F(x,y 0 ) ≤ F(x 0 ,y 0 );
∀ y G(x 0 ,y) ≤ G(x 0 ,y 0 ).
(6.1)
(6.2)
Смысл ситуации равновесия состоит в том, что каждому игроку невыгодно односторонне отступать от входящей в ситуацию стратегии. Таким образом, понятие ситуации равновесия обобщает понятие седловой точки матричной игры.
|
|
|
Представляет определенный интерес оптимальность в смысле,
отличном от того, который дает понятие ситуации равновесия.
Определение. Пара стратегий (x 0 ,y 0)называется оптимальной по
Парето, если не существует другой пары стратегий (x, y), такой, что
F (x, y 0) ≥ F (x 0, y 0), G (x 0, y) ≥ G (x 0, y 0)
(притом хотя бы одно из неравенств является строгим).
Содержательно оптимальность по Парето означает следующее: нет другой ситуации, которая была бы строго предпочтительнее для обоих игроков.
Формальное различие между ситуацией равновесия и ситуацией, оптимальной по Парето, следующее: в первой ни один игрок, действуя в одиночку, не может увеличить своего собственного выигрыша, а во второй
оба игрока, действуя совместно, не могут (даже нестрого) увеличить выигрыш каждого. Выбор Парето-оптимальной пары стратегий может приводить к ситуациям, более выгодным для обоих участников, чем
ситуации равновесия.
Для матричных игр ситуация равновесия и Парето-оптимальность – равносильные понятия. Сколько-нибудь подробное изложение достаточно важной теории Парето-оптимальности не входит в пособие.
ТЕОРЕМА 6.1. Каждая биматричная игра имеет по крайней мере одну ситуацию равновесия.
Доказательство. Сначала построим отображение Т множества пар стратегий в себя так, чтобы неподвижные точки отображения совпадали с
ситуациями равновесия. Положим для (x, y)
ci = max(F (ei, y) − F (x, y),0),
|
|
|
|
i =1,..., n,
|
x + c
y j + d j
|
i n
i =1,..., n, '
, j =1,..., m.
m
1 + ∑ ck
k =1
1 +
|
∑ dk
|
Нетрудно проверить, что
x ' = (x ',..., x ') и
y ' = (y ',..., y '
|
стратегии. Покажем, что Т (x, y)=(x, y) тогда и только тогда, когда (x, y)-
ситуация равновесия.
Пусть (x 0, y 0) - ситуация равновесия. Тогда
F (ei, y 0) ≤ F (x 0, y 0)
'
при
всех i =1,…, n и, следовательно,
'
ci = 0, x 0 i
= x 0 i.
Аналогично,
d j = 0, y 0 j
= y 0 j
при всех j =1,…, m. Таким образом, действительно,
Т (x 0, y 0) =(x 0, y 0).
Предположим, что (x 0, y 0) не является ситуацией равновесия. Тогда
либо существует x, для которого
F (x, y 0) > F (x 0, y 0), либо существует y,
для которого
G (x 0, y) > G (x 0, y 0). Пусть имеет место первый случай. Тогда
существует i 0, для которого
F (ei 0, y 0) > F (x 0, y 0). В самом деле, в
противном случае мы имеем
F (ei
, y 0) ≤ F (x 0, y 0)
при всех i =1,…, n, откуда
вытекает неравенство
n
∑
i =1
|
i
, y 0) ≤
n
∑
i =1
|
неравенству
F (x, y 0) ≤ F (x 0, y 0), которое противоречит нашему исходному
n
предположению. Для данного i 0
ci 0
> 0 и, следовательно,
∑ ck
> 0.
Теперь покажем, что существует i 1, для которого
F (ei, y 0) ≤ F (x 0, y 0).
Пусть
F (ei, y 0) > F (x 0, y 0)
при всех i =1,…, n. Тогда справедливо
n n
неравенство
∑ x 0 iF(ei, y 0 ) >
i =1
∑ x 0 iF(x 0, y 0 ), эквивалентное неравенству
i =1
F (x 0, y 0) > F (x 0, y 0).
Приходим к противоречию, доказывающему справедливость нашего
утверждения.
Итак,
xi
F (ei 1, y 0) ≤ F (x 0, y 0) и, следовательно,
ci 1 = 0
. Но тогда
|
|
|
i 1 n
1+ ∑ ck
k =1
≠ xi 1,
' ≠ x 0
и Т (x 0, y 0) ≠ (x 0, y 0), что и требовалось
доказать.
Итак, мы построили отображение множества пар стратегий в себя, такое, что неподвижные точки отображения совпадают с ситуациями равновесия.
Заметим, что множество пар стратегий является ограниченным,
замкнутым и выпуклым, а построенное отображение непрерывным. Тогда можно применить следующую теорему:
ТЕОРЕМА БРАУЭРА. Пусть S - компактное выпуклое
подмножество k -мерного евклидового пространства; f – непрерывная функция, отображающая S в себя. Тогда существует по крайней мере одна
такая точка s ∈ S, что f(s)=S.
Итак, отображение Т имеет по крайней мере одну неподвижную
точку. Следовательно, биматричная игра имеет по крайней мере одну ситуацию равновесия.
Доказательство теоремы 6.1 завершено.
В чистых же стратегиях ситуация равновесия существует в биматричной игре не всегда (как в матричной игре не всегда есть седловые точка). Рассмотрим примеры поиска чистых ситуаций равновесия.
Пример6.1.
⎛7 5 1 ⎞
|
|
⎛3 2 5 ⎞
|
|
|
A = ⎜6
⎝4
3 2 ⎟,
0 ⎠
B = ⎜0
⎝1
6 7 ⎟.
6 ⎠
Позиции максимумов в столбцах матрицы А – (1,1),(1,2),(3,3). Позиции
максимумов в строках матрицы В – (1,3),(2,3),(3,2). Соответствующие значения обведены кружками. Эти два множества позиций не пересекаются, следовательно, ситуации равновесия в чистых стратегиях нет.
⎛8
⎜
|
⎝2
4 6 ⎞
⎟
|
1 ⎠
⎛4 4
⎜
|
⎝5 6
5⎞
⎟
⎠
Позиции максимумов в столбцах матрицы А – (1,1),(2,2),(2,3). Позиции максимумов в строках матрицы В – (1,1),(1,2),(2,2),(3,3). Пересечение этих двух множеств – (1,1) и (2,2). Таким образом, есть две ситуации равновесия в
чистых стратегиях - (e 1, f 1)
и (e 2, f 2 ).
В антагонистических играх седловые точки являются эквивалентными, а оптимальные стратегии взаимозаменяемыми. Приведем примеры, показывающие, что ситуации равновесия биматричных игр в общем случае этими свойствами не обладают.
Пример6.2. Семейный спор.
|
|
|
⎛4 0 ⎞
A = ⎜ ⎟,
⎝0 1 ⎠
⎛1 0 ⎞
B = ⎜ ⎟.
⎝0 4 ⎠
Интерпретация этого примера такова. "Игроки" - жена и муж. Каждый игрок имеет две чистые стратегии: 1 - пойти в цирк и 2 - пойти в театр. Жена предпочитает цирк, муж - театр, но каждый предпочитает совместное времяпрепровождение раздельному. В соответствии с этими предпочтениями и расставлены выигрыши, представленные в балльной шкале. В этой игре имеется две ситуации равновесия в чистых стратегиях:
(e 1, f 1)и (e 2 ,f 2 ). Однако они не являются эквивалентными:
4= F (e 1, f 1) ≠ F (e 2, f 2) =1,
1= G (e 1, f 1) ≠ G (e 2, f 2) = 4.
Стратегии же,
входящие в ситуации равновесия, не взаимозаменяемы: пары стратегий
(e 1, f 2)
и (e 2 ,f 1 )
ситуациями равновесия не являются. Таким образом,
несмотря на наличие в данной игре двух ситуаций равновесия в чистых стратегиях, "решения" (в интуитивном смысле) она не имеет и исход игры предсказать трудно.
Известна задача о разделе ста долларов. Два игрока должны поделить между собой эту сумму. Стратегия каждого – назвать то число долларов,
которое он хочет получить, то есть число от 0 до 100. Если два названных числа в сумме не превышают 100, раздел состоялся. Иначе оба игрока ничего не получают. Даже если разрешить игрокам называть только целые числа,
игра будет иметь 101 ситуацию равновесия в чистых стратегиях. Эти ситуации представляют все возможные варианты полного раздела суммы. Такой пример снова подчеркивает уязвимость ситуации равновесия как решения игры.
Даже в том случае, когда в биматричной игре имеется единственная ситуация равновесия, ее зачастую трудно считать решением игры. Это подтверждается следующим примером.
Пример 6.3. Дилемма заключенного. Конкурс на реализациюпроекта.
⎛ − 8
A = ⎜
⎝−10
− 2⎞
⎟,
− 4⎠
⎛− 8
B = ⎜
⎝− 2
−10⎞
⎟.
− 4 ⎠
Интерпретируется этот пример так. "Игроками" являются двое заключенных, обвиняемых в совершении тяжелого преступления, их стратегиями - сознаваться или не сознаваться. Если оба сознаются (в матрице это 1-я строка и 1-й столбец), то получат большой срок заключения, но не максимальный. Если оба не сознаются (2-я строка и 2-й столбец), то их осудят за менее тяжкие преступления, в которых они уже уличены. Наконец,
|
|
|
если сознается только один, то его срок заключения будет значительно снижен, а другой получит максимальный срок. (Числа в матрицах - это сроки
заключения, взятые с противоположным знаком.) В этой игре
(e 1, f 1) -
единственная ситуация равновесия. Ситуация же (e 2, f 2 ), более выгодная для обоих игроков, равновесной не является, так как каждому игроку выгодно односторонне отступить от стратегии, в нее входящей. Достаточно легко найти экономический пример матрицы с подобной расстановкой предпочтений (то есть с элементами матриц, находящимися в таком же порядке по числовым значениям) – конкурс на реализацию проекта. Две фирмы, борющиеся за заказ на определенную работу, могут выбрать два варианта - подать развернутую программу(1-я стратегия) или простую заявку(2-я стратегия). Согласно правилам при одинаковом выборе конкурентов заказ и доход делятся пополам, а в другом случае предпочтение отдается фирме, подавшей подробную заявку. На реализацию проекта победителям (одному или двоим) выделяется 10 тысяч долларов. Технические затраты на простую заявку - 1 тысяча долларов, на развернутую программу - 3 тысячи долларов.
⎛ 2 7 ⎞
⎛2 −1⎞
A = ⎜
⎟, B = ⎜ ⎟.
⎝−1 4 ⎠
⎝7 4 ⎠
Эти два примера (дилемма заключенного и борьба конкурсантов) характеризуют важную особенность биматричных игр – возможность наличия противоречия между выгодностью и устойчивостью. В обоих
случаях для обоих игроков выгодной является ситуация
(e 2 ,f 2 ), а
устойчивой -
(e 1, f 1). Под неустойчивостью мы понимаем выгодность для
одного из игроков одностороннего отклонения от ситуации. Выход здесь – в кооперации игроков.
Алгоритм поиска ситуации равновесия для биматричной игры
произвольной размерности достаточно сложен. Поэтому дадим описание ситуаций равновесия только в биматричных играх размерности 2×2. Такая игра задается парой матриц
⎛ a a ⎞
⎛ b b ⎞
A = ⎜ 11
12 ⎟,
B = ⎜ 11
12 ⎟.
⎝ a 21
a 22 ⎠
⎝ b 21
b 22 ⎠
Примем без доказательства следующую
ТЕОРЕМУ 6.2. Если в биматричной игре Г элементы, стоящие в одном столбце матрицы А, и элементы, стоящие в одной строке матрицы В, попарно
различны, то ситуации равновесия могут быть либо чистыми, либо вполне смешанными (то есть такими, в которых обе чистые стратегии применяются
с положительными вероятностями). Вполне смешанная ситуация (x, y), где
x = (x 1, x 2), y = (y 1, y 2)
будет ситуацией равновесия в игре Г при
выполнении следующих условий:
⎧ b 11 x 1 + b 21 x 2
⎪
= b 12 x 1 + b 22 x 2;
⎨ x 1, x 2
⎪
> 0;
(6.3)
⎩ x 1 + x 2
= 1.
⎧ a 11 y 1 + a 12 y 2
⎪
= a 21 y 1 + a 22 y 2;
⎨ y 1, y 2
⎪
> 0;
(6.4)
⎩ y 1 + y 2
= 1.
Введем следующие обозначения:
β = b 22
− b 21
; (6.5)
(b 11 + b 22) − (b 12
+ b 21)
α = a 22
− a 12
. (6.6)
(a 11 + a 22) − (a 12
+ a 21)
Получаем, что система (6.3) имеет решение (единственное) тогда и
только тогда, когда
0 < β
<1, причем в этом случае решение системы (6.3)
есть
x 1 = β, x 2
=1− β.
Аналогичным образом получаем, что система (6.4)
имеет решение (единственное) тогда и только тогда, когда
0 <α<1, и в этом
случае решение системы (6.4) есть y 1 =α, y 2
=1−α.
Итак, если
0 <α, β<1, то игра Г имеет вполне смешанную, причем
единственную, ситуацию равновесия
(x 0, y 0),
где
x 0 = (β,1− β),
y 0 = (α,1−α).
Например, для игры «Семейный спор» смешанная ситуация равновесия находится так:
α= 1 − 0
= 1,
β= 4 − 0 = 4, 0
4 1
⎜, ⎟,
0 1 4
⎜, ⎟.
5 − 0 5
5 − 0
x = ⎛ ⎞
5 ⎝ 5 5 ⎠
y = ⎛ ⎞
⎝ 5 5 ⎠
Выигрыш обоих игроков при использовании такой смешанной
стратегии составит 4.
Пример 6.4. Борьба за рынки сбыта.
Фирма а намерена сбыть партию товара на одном из двух рынков,
контролируемых более крупной фирмой b. С этой целью она проводит подготовительную работу, связанную с определенными затратами. Если
фирма b разгадает - на каком из рынков фирма а будет продавать свой товар,
она примет контрмеры и воспрепятствует "захвату" рынка (этот вариант означает поражение фирмы а); если нет, то фирма а одерживает победу.
Предположим, что для фирмы а проникновение на первый рынок более выгодно, чем проникновение на второй, но и борьба на первом рынке требует
от нее больших средств. Например, победа фирмы а на первом рынке
приносит ей вдвое большую прибыль, чем победа на втором, но зато поражение на первом рынке полностью ее разоряет. Составим математическую модель этого конфликта, считая фирму а игроком 1 и фирму b игроком 2. Стратегии игрока 1: первая - проникновение на рынок 1, вторая
- проникновение на рынок 2; стратегии игрока 2: первая - контрмеры на рынке 1, вторая - контрмеры на рынке 2. Пусть для фирмы а ее победа на 1-м рынке оценивается в 2 единицы, а победа на 2-м рынке - в 1 единицу; поражение фирмы а на 1-м рынке оценивается в -10, а на 2-м в -1. Для фирмы b ее победа составляет соответственно 5 и 1 единицу, а поражение -2 и -1.
Получаем в итоге биматричную игру Г с матрицами выигрышей
⎛−10
A = ⎜
2 ⎞ ⎛ 5
|
|
− 2 ⎞
⎟.
⎝ 1 −1⎠
⎝−1 1 ⎠
По теореме 6.2 эта игра может иметь либо чистые, либо вполне смешанные ситуации равновесия. Ситуаций равновесия в чистых стратегиях здесь нет (содержательно этот факт можно объяснить следующим рассуждением: если стратегия фирмы а была разгадана фирмой b, то в этой ситуации отклонение выгодно для фирмы а; в противном случае отклонение выгодно для фирмы b). Убедимся теперь, что данная игра имеет вполне смешанную ситуацию равновесия. Действительно, из (6.6) и (6.5) находим
α= −1 − 2
−11 − 3
= 3,
14
β= 1 +1
6 + 3
= 2.
Итак, рассматриваемая игра имеет единственную ситуацию равновесия
⎛2 7 ⎞
⎛ 3 11 ⎞
(x 0, y 0),
где
x 0 = ⎜, ⎟,
9 9
y 0 = ⎜, ⎟.
14 14
Она может быть реализована при
⎝ ⎠ ⎝ ⎠
многократном повторении игры (то есть при многократном воспроизведении описанной ситуации) следующим образом: фирма а должна использовать чистые стратегии 1 и 2 с частотами 2/9 и 7/9, а фирма b - чистые стратегии 1 и 2 с частотами 3/14 и 11/14. Любая из фирм, отклонившись от указанной смешанной стратегии, уменьшает свой ожидаемый выигрыш (однако, это не означает, как в случае антагонистических игр, что другая фирма увеличивает при этом свой ожидаемый выигрыш).
Пример 6.5. Соперничество в области технологического лидерства.
Этот пример примитивен в вычислительном плане, но содержателен. Предприятие 1 ранее обладало технологическим превосходством, но в настоящее время располагает меньшими финансовыми ресурсами для научных исследований и разработок (НИР), чем его конкурент. Оба предприятия должны решить, стоит ли пытаться с помощью крупных капиталовложений добиться доминирующего положения на мировом рынке в соответствующей технологической области. Если оба конкурента вложат в дело крупные средства, то перспективы на успех у предприятия 1 будут лучше, хотя оно и понесет большие финансовые расходы (как и предприятие
2). Эта ситуация представлена платежами с отрицательными значениями.
Первая стратегия у предприятия 1 – низкие затраты на НИР, у предприятия
2 – неучастие в технологической конкуренции. Вторая стратегия у каждого игрока – высокие затраты на НИР. Для предприятия 1 лучше всего было бы, если бы предприятие 2 отказалось от конкуренции. Его выгода в таком случае составила бы 3 (платежа). С большой вероятностью предприятие 2
выиграло бы соперничество, когда предприятие 1 приняло бы урезанную программу инвестиций, а предприятие 2 – более широкую.
⎛3
A = ⎜
1 ⎞ ⎛ 0 3 ⎞
⎟, B = ⎜ ⎟.
⎝0 −1⎠
⎝0 − 2 ⎠
Анализ матрицы показывает, что равновесие в чистых стратегиях наступает при высоких затратах на НИР предприятия 2 и низких предприятия
1. При любом другом раскладе у одного из конкурентов появляется резон отклониться от стратегической комбинации: так, для предприятия 1 предпочтителен сокращенный бюджет, если предприятие 2 откажется от
участия в соперничестве; в то же время предприятию 2 известно, что при низких затратах конкурента ему выгодно инвестировать в НИР. Предприятие, имеющее технологическое преимущество, может прибегнуть к
анализу ситуации на базе теории игр, чтобы, в конечном счете, добиться оптимального для себя результата. С помощью определенного сигнала оно должно показать, что готово осуществить крупные затраты на НИР. Если такой сигнал не поступил, то для предприятия 2 ясно, что предприятие 1
выбирает вариант низких затрат. О достоверности сигнала должны свидетельствовать обязательства предприятия, например, решение предприятия 1 о закупке новых лабораторий или о найме на работу
дополнительного научно-исследовательского персонала.
Рассмотрим вкратце кооперативное поведение игроков в биматричных играх. Безусловно, чем больше игроков, тем шире возможности для создания
коалиций, но и в биматричном случае противники могут в какой-то мере успешно координировать свои действия.
Можно показать, что даже если ситуация равновесия Парето-
оптимальна, то и тогда возможны случаи, когда одна ситуация равновесия выгодна одному игроку, а другая – другому. Разрешим игрокам совершать совместные действия и, расширив, таким образом, множество стратегий, будем искать оптимальные решения на этом множестве.
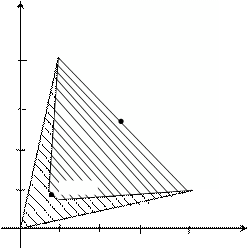
Вернемся к игре «Семейный спор». Множество точек,
соответствующих всем выигрышам в смешанных стратегиях, заштриховано
G на рис. 6.1. Есть две чистых ситуации равновесия и одна вполне смешанная с
(1,4)
вектором выигрышей
⎛ = 4
⎜
⎝5
= 4 ⎞
, ⎟. Как
5 ⎠
3 (5/2,5/2)
(4/5,4/5)
(4,1)
видно из рисунка, чистые ситуации равновесия Парето-оптимальны. Если игра повторяется многократно, то игрокам имеет смысл с вероятностью
0.5 выбирать каждую из двух чистых равновесных стратегий. Тогда средний
выигрыш каждого составит 2.5
0 1 2 3 4
Рис. 6.1
единицы. Но соответствующая ситуации точка не лежит во множестве
точек, определяемом правилами бескоалиционной биматричной игры, т.е. не может быть реализована, если игроки выбирают свои стратегии независимо друг от друга.
Совместной смешанной стратегией называют смешанную стратегию,
на которую согласны оба игрока (Это вероятностное распределение на множестве всевозможных пар (i,j), не обязательно порожденное независимым
случайным выбором чистых стратегий игроками 1 и 2). Предполагается, что такие стратегии могут быть реализованы посредником в переговорах до начала игры. Обозначим буквой M совместную смешанную стратегию в игре
Г. Тогда ожидаемые выигрыши F (M)
и G(M) игроков 1 и 2 соответственно
определяются как математические ожидания выигрышей на чистых стратегиях:
n m n m
F (M)= ∑∑ aij μ ij; G (M)= ∑ ∑ bij μ ij.
i =1 j =1
i =1 j =1
В биматричной игре размерности n×m любая совместная смешанная стратегия задается матрицей n×m, элементы матрицы неотрицательны, их
сумма равна 1. Элемент
μ ij −
вероятность того, что 1-й игрок выберет i -ю
стратегию, а 2-й игрок – j -ю стратегию.
Геометрическое
изображение множества точек, G
соответствующего множеству векторов выигрышей в 4 совместных смешанных стратегиях для игры «Семейный
спор» приведено на рис. 6.2. Это 3
выпуклая оболочка множества точек возможных выигрышей в 2 чистых стратегиях. Совместной смешанной стратегии M* = 1
(1,4)
(4/5,4/5)
(5/2,5/2)
(4,1)
⎜ 2 ⎟
соответствует 0
1 2 3 4 F
⎝ 2 ⎠
Рис. 6.2
оптимальный по Парето вектор
выигрышей (5/2,5/2). Таким образом, M* может быть рекомендована в качестве решения игры «Семейный спор».
Для игры в совместных смешанных стратегиях также вводится понятие ситуации равновесия. В биматричной игре Г размерности n×m
обозначим через M = {μ ij }совместное вероятностное распределение на парах
(i, j), i =1,...., n
j =1,...., m.
Для каждого i (или j) введем
μ i (j)(или ν j (i)соответственно)
- условную вероятность реализации j (или i
соответственно). По определению эти вероятности таковы:
⎧
⎪
⎪
μ (j) = ⎨
μ ij
m,
∑ μ ik
=
m
если ∑ μ ik ≠ 0
k =1
.
i k 1
⎪ m
⎪0,
⎪⎩
если ∑ μ ik = 0
k =1
⎧
⎪
⎪
() =
μ ij
n,
∑ μ kj
n
|
k =1
ν ji ⎨
⎪
k =1.
n
⎪0,
⎪⎩
если ∑ μ kj = 0
k =1
Определение. Будем говорить, что M* = {μ* }- ситуация равновесия в
совместных смешанных стратегиях в игре Г, если выполнены неравенства
m m
∑ aij μ i (j)≥ ∑ akj μ k (j)
*
j =1
n
*
j =1
n
(6.7)
∑ bij ν j (i)≥∑ bil ν l (i)
*
i =1
*
i =1
∀ i, k ∈ {1,...., n }, j, l ∈ {1,...., m }.
Игру Г в совместных смешанных стратегиях можно интерпретировать
так. Пусть игроки договорились об использовании стратегии
M *, и после
реализации случайного механизма 1-й игрок получил стратегию
i, а 2-й –
стратегию
j. Каждый игрок знает только свою реализацию. Каждый может
не согласиться с реализацией, отведенной ему, и выбрать соответственно стратегию k или l. Тогда любому из игроков невыгодно односторонне
отклониться от предложенной реализации, если
M * - равновесна (это
следует из (6.7), где слева в неравенствах стоят выигрыши игроков в случае согласия с реализацией i(j)).
Примем без доказательства следующую
ТЕОРЕМУ 6.3.
Множество ситуаций равновесия в совместных смешанных стратегиях биматричной игры размерности n×m является непустым выпуклым
компактом в пространстве
Rn + m.
Если (x, y)- пара смешанных стратегий игроков 1 и 2, то определяемая
по ним ситуация M = {μ ij }в совместных смешанных стратегиях будет
равновесной тогда и только тогда, когда (x, y)- ситуация равновесия в игре
Г.
С помощью этой теоремы можно проверить, что, например, в игре
«Семейный спор» стратегия M* = ⎜ 2
⎞
⎟ - равновесна.
⎝ 2 ⎠
Итак, очевидно, что координация действий приносит ощутимые выгоды обоим игрокам. При определенных условиях часть выигрыша по договоренности может также передаваться от одного игрока к другому.
Возникает естественный вопрос о том, как разумным игрокам прийти к соглашению при совместном выборе решения в ходе переговоров. Но ответ
на этот вопрос выходит за рамки пособи
