Ориентируемые кривые. Криволинейные интегралы первого и второго рода, их свойства и вычисление. Соленоидальное поле и его свойства

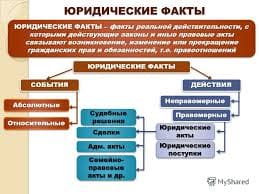
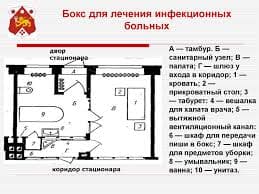
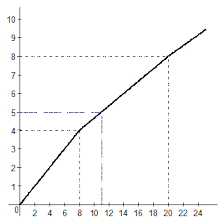
Соленоидальное поле и его свойства

Поле называется соленоидальным в области если Это означает, что в либо нет источников и стоков, либо их суммарная мощность равна нулю.

Соленоидальное поле обладает следующими свойствами (ниже предполагается, что односвязная область, а поле непрерывно дифференцируемо в):

1. Если поле соленоидально в области то поток через любую кусочно гладкую замкнутую поверхность равен нулю.

2 (закон сохранения интенсивности векторной трубки). Если поле соленоидально в области и – произвольная векторная трубка этого поля, то поток через любое поперечное сечение этой трубки постоянен (т.е. не зависит от поперечного сечения.)

Докажем только свойство 1. Так как поле соленоидально в области то а значит, по теореме Остроградского-Гаусса имеем

ч.т.д

Если на кривой указан порядок следования её точек, то кривая называется ориентированной кривой. Укажем на наиболее распространённые типы ориентации.

а) Кривая – спрямляемая дуга без точек самопересечений. Ориентация: указание начальной точки и конечной точки (точки следуют от к – положительная ориентация, противоположное направление – отрицательная ориентация).

б) Если кривая задана параметрически уравнениями

то положительная ориентация задается по возрастанию параметра, а отрицательная ориентация – по убыванию параметра

в) Если кривая задана параметрически уравнениями причем функции непрерывно дифференцируемы на отрезке и то каждая точка ориентируется по направлению вектора положительная ориентация; если точки кривой направлены по направлению вектора то кривая будет иметь отрицательную ориентацию.

Кривые с положительной ориентацией обозначаются обычно а с отрицательной ориентацией – Перейдем теперь к понятию криволинейного интеграла. Сначала дадим определение криволинейного интеграла первого рода (по длине дуги).

Пусть в пространстве задана некоторая непрерывная спрямляемая (простая) дуга и пусть функция определена на этой дугу. Произведем разбиение дуги на частичные дуги. Обозначим через длину дуги, а через диаметр разбиения Пусть произвольная точка дуги.

Определение 1. Если существует конечный предел интегральных сумм:

и этот предел не зависит от вида разбиения и выбора точек, то его называют криволинейным интегралом первого рода (по длине дуги) и обозначают При этом функция называется интегрируемой вдоль дуги

Криволинейный интеграл обладает всеми свойствами обычных интегралов. Перечислим их (везде ниже – кусочно гладкая спрямляемая дуга):

(Линейность). Если функции интегрируемы вдоль дуги, то и функция также интегрируема вдоль дуги и имеет место равенство

(Аддитивность). Если дуга разбита точкой на две дуги и и если функция интегрируема на дуге то она интегрируема и на дугах и (и обратно). При этом имеет место равенство

(Теорема о среднем). Если функция непрерывна на ограниченной кусочно гладкой спрямляемой дуге, то найдется точка такая, что

где длина дуги.

Криволинейный интеграл первого рода не зависит от ориентации дуги, т.е.

Последнее свойство следует из того, что в интегральной сумме для криволинейного интеграла длина дуги не зависит от ориентации дуги.

Теорема 1 (о вычислении криволинейного интеграла первого рода). Пусть дуга задана параметрически уравнениями причем функции непрерывны на отрезке. Пусть, кроме того, функция непрерывна на дуге. Тогда

.

Доказательство. Воспользуемся определением криволинейного интеграла:

Пусть Из первого семестра нам известно, что По теореме о среднем для обычного интеграла найдётся точка такая, что

Подставляя это в интегральную сумму и учитывая, что в силу непрерывности функции будет,

получим

Теорема доказана.

Физический смысл криволинейного интеграла первого рода. Если плотность стержня в точке то масса этого стержня (рассуждения те же самые, что и при выяснении физического смысла двойного интеграла).

Перейдём теперь к понятию криволинейного интеграла второго рода (по координатам).Пусть – ориентированная дуга (можно считать, что она ориентирована от начала до конца) и пусть векторное поле определено на этой дуге. Произведем разбиение дуги на частичные дуги точками в направлении ориентации дуги (т.е. точка следует за точкой если). Обозначим Возьмем произвольно точку и составим интегральную сумму

Определение 2. Если существует конечный предел интегральных сумм:

и он не зависит от вида разбиения и выбора точек то его называют криволинейным интегралом второго рода от векторного поля

вдоль ориентированной дуги и обозначают При этом поле называется интегрируемым на дуге.

Заметим, что в криволинейном интеграле второго рода в качестве подынтегральной функции выступает скалярное произведение

Ясно, что такой интеграл обладает всемы свойствами криволинейного интеграла первого рода, за исключением свойства Интеграл второго рода зависит от ориентации кривой:

Это вытекает из того, что при изменении ориентации кривой в интегральной сумме вектор заменяется на противоположный вектор

Приведем без доказательства следующее утверждение.

Теорема 2 (о вычислении криволинейного интеграла второго рода). Пусть дуга задана параметрически уравнениями причем функции непрерывны на отрезке и Пусть, кроме того, векторное поле

непрерывно на дуге и эта дуга ориентирована по возрастанию параметра Тогда

где

Физический смысл криволинейного интеграла второго рода состоит в следующем: если сила, действующая на материальную точку, то интеграл равен работе силового поля по перемещению точки вдоль пути.