2014-02-02
1213
ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ВЫБОРКИ
План
1. Эмпирическая функция распределения
2. Числовые характеристики генеральной совокупности
3. Точечные оценки числовых параметров генеральной совокупности
4. Распределение выборочных средних
Как известно, закон распределения случайной величины можно задавать различными способами. Дискретную случайную величину можно задать с помощью ряда распределения или интегральной функции, а непрерывную случайную величину – с помощью или интегральной, или дифференциальной функции. Рассмотрим выборочные аналоги этих двух функций.
Пусть имеется выборочная совокупность значений некоторой случайной величины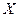 
объема 
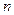и каждому варианту из этой совокупности поставлена в соответствие его частость. Пусть далее, 
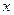– некоторое действительное число, а 
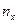– число выборочных значений случайной величины 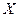, меньших 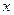.Тогда число 
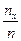является частостью наблюдаемых в выборке значений величины X, меньших 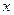, т.е. частостью появления события 
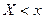. При изменении x в общем случае будет изменяться и величина 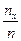. Это означает, что относительная частота 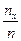является функцией аргумента 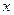. А так как эта функция находится по выборочным данным, полученным в результате опытов, то ее называют выборочной или эмпирической.
|
|
|
Определение 15.1. Эмпирической функцией распределения (функцией распределения выборки) называют функцию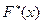 
, определяющую для каждого значения x относительную частоту события .
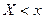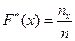(15.1)
В отличие от эмпирической функции распределения выборки функцию распределения F(x) генеральной совокупности называют теоретической функцией распределения. Различие между ними состоит в том, что теоретическая функция F(x) определяет вероятность события 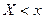, а эмпирическая – относительную частоту этого же события. Из теоремы Бернулли следует
, 
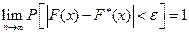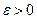(15.2)
т.е. при больших 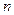вероятность 
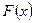и относительная частота события 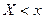, т.е. 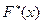мало отличаются одно от другого. Уже отсюда следует целесообразность использования эмпирической функции распределения выборки для приближенного представления теоретической (интегральной) функции распределения генеральной совокупности. Функция 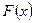и 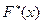обладают одинаковыми свойствами. Это вытекает из определения функции.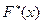
Свойства 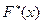: 1) 
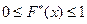; 2) 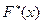– неубывающая функция; 3)
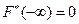; 4)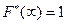 
.
Пример 15.1. Построить эмпирическую функцию по данному распределению выборки:
Варианты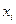 
| |||
Частоты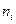 
|
Решение: Найдем объем выборки n= 12+18+30=60. Наименьшая варианта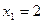 
, следовательно, 
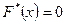при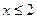 
. Значение 
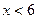, а именно 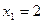наблюдалось 12 раз, следовательно:
=
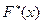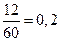при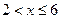
.
Значение x< 10, а именно 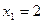и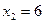 
наблюдались 12+18=30 раз, следовательно, = 
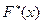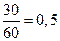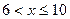при 
. При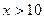 
.
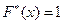Искомая эмпирическая функция распределения:
|
|
|
=
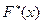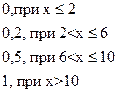
График представлен на рис. 15.1
 |
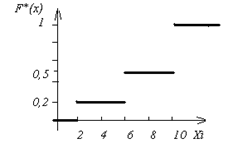Рис. 15.1
