Пример 5.
Пример 4.
Пример 3.
Пример 2.
Пример 1.
Найти 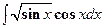 .
.
Сделаем подстановку 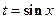 , тогда
, тогда 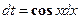 и, следовательно,
и, следовательно, 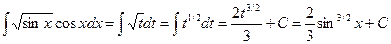
Найти 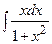 . Полагаем
. Полагаем 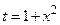 , тогда
, тогда 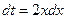 и
и
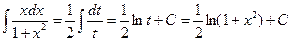
Найти 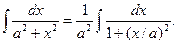 Полагаем
Полагаем 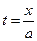 ; тогда
; тогда 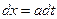 ,
,
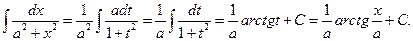
Найти 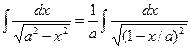 . Полагаем
. Полагаем 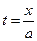 ; тогда
; тогда 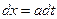 ,
,
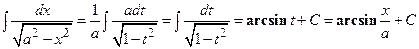 (предполагается, что a>0).
(предполагается, что a>0).
Найти 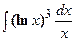 . Полагаем
. Полагаем 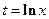 , тогда
, тогда 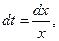
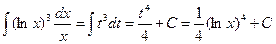 .
.
Найти 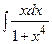 . Полагаем
. Полагаем 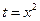 , тогда
, тогда 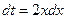 ,
,
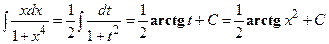
Метод замены переменных является одним из основных методов вычисления неопределенных интегралов. Успех интегрирования зависит в значительной степени от того, сумеем ли мы подобрать такую удачную замену переменных, которая упростила бы данный интеграл. Изучение методов интегрирования сводится к выяснению того, какую надо сделать замену переменной при том или ином виде подынтегрального выражения.
- Метод интегрирования по частям
Пусть 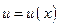 и
и 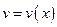 - функции имеющие непрерывные производные. Тогда
- функции имеющие непрерывные производные. Тогда 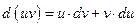 . Интегрируя это равенство, получаем
. Интегрируя это равенство, получаем
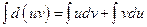 или
или 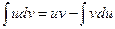 .
.
Полученная формула называется формулой интегрирования по частям. Она дает возможность свести вычисление интеграла 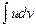 к вычислению интеграла
к вычислению интеграла 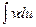 , который может оказаться существенно более простым, чем исходный.
, который может оказаться существенно более простым, чем исходный.
Интегрирование по частям состоит в том, что подынтегральное выражение заданного интеграла представляется каким – либо образом в виде произведения двух сомножителей u и dv; затем, после нахождения v и du, используется формула интегрирования по частям.
Некоторые типы интегралов, которые удобно вычислять методом интегрирования по частям.
- Интегралы вида
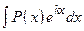 ,
, 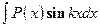 ,
, 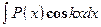 , где
, где 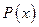 - многочлен, k – число. Удобно положить
- многочлен, k – число. Удобно положить 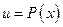 , а за dv обозначить остальные сомножители.
, а за dv обозначить остальные сомножители. - Интегралы вида
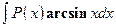 ,
, 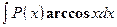 ,
, 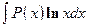 ,
, 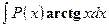 ,
, 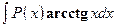 . Удобно положить
. Удобно положить 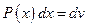 , а за u обозначить остальные сомножители.
, а за u обозначить остальные сомножители. - Интегралы вида
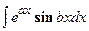 ,
, 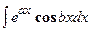 , где a и b – числа. За
, где a и b – числа. За 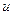 можно принять функцию
можно принять функцию 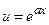 .
.
 2014-02-02
2014-02-02 376
376








