Линейная независимость, размерность и базис линейного пространства

Элементы 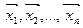линейного пространства называются линейно-зависимыми, если существуют такие скаляры 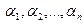, не все равные 0, что имеет место равенству:

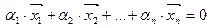
Очевидно, что в этом случае любой из этих элементов можно выразить линейной комбинацией, например:

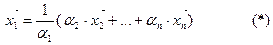
Этого нельзя сделать, если равенство (*) не выполняется, или при 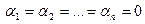. В таком случае элементы 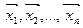линейно-независимы. Количество линейно-независимых элементов, присутствующих в линейном пространстве, определяет размерность этого пространства. Линейное пространство, в котором можно найти n-независимых элементов, а любые n+1-независимые элементы являются линейно-зависимые, называется n-мерным. Если можно найти бесконечное число линейно-независимых элементов, то пространство называется бесконечномерным. Набор n-линейных векторов 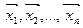линейного пространства называется полным, если любой вектор 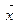может быть выражен в виде:

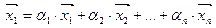
Полный набор линейно-независимых векторов пространства называется его базисом. Число векторов, содержащихся в базисе линейного пространства, называют размерностью базиса. При этом понятия размерности базиса и размерности пространства совпадают.

В одном и том же векторном пространстве может существовать несколько различных базисов (до бесконечности), но все они содержат одинаковое количество векторов. В общем случае, произвольный вектор 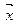линейного пространства может быть выражен в виде линейной комбинации m-векторов этого пространства, не все из которых являются линейно-независимыми. Однако, можно строго показать, что в этом случае количество слагаемых m > n. Т.о., наиболее рациональным является представление вектора на основе линейной комбинации полного набора линейно-независимых векторов.

Пример:

Линейное пространство векторов на плоскости является двумерным.

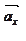
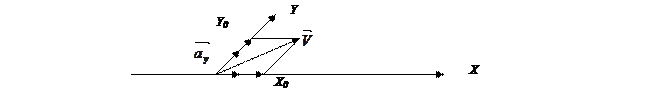
Действительно, если обозначить единичные векторы вдоль осей X и Y соответственно a_x и a_y, то произвольный вектор V можно определить как 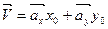, где х₀, y₀ - скаляры (координаты вектора). Вектора 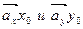, расположенные вдоль осей координат, являются линейно-независимыми, т.к. равенство 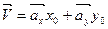возможно только при нулевых значениях чисел х₀ и y₀ . В то же время любой другой вектор на плоскости 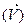может быть однозначно определен своим составляющими вдоль оси x и y. Система координат x и y, определенная векторами ax и ay, представляет базис данного пространства. Поскольку угол между осями координат может быть произвольным, возможно бесконечное множество различных вариантов построения базиса данного пространства, однако, в любом случае, базис будет представлять собой систему из двух линейно-независимых векторов. Если в качестве элементов пространства рассматривать множество направленных отрезков в геометрическом пространстве, то, проводя аналитические рассуждения, можно прийти к выводу, что данное пространство является трехмерным. При этом всякую упорядоченную тройку действительных чисел x₀, y₀, z₀ можно рассматривать как координаты радиус-вектора трехмерного пространства в некотором базисе (системе координат).

Рассматривая совокупность n-вещественных чисел {x₀, x₁, …, x_n}, можно считать их координатами радиус-вектора некоторого абстрактного n-мерного линейного пространства. Это пространство при n>3, не имеет физического прообраза, доступного нашему чувственному восприятию, однако является весьма полезным при рассмотрении ряда вопросов ТЭС. Непрерывная функции времени, дискретизированная на интервале (–T/2; T/2) в n-точках может быть представлена в n-мерном пространстве радиус-вектора, координаты которого определяются дискретными значениями сигналов. При 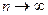т.о. можно представить и недискретизированную непрерывную функцию f(t).