Пусть наблюдаемая случайная величина 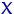 зависит от случайной величины или случайного вектора
зависит от случайной величины или случайного вектора 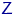 . Значения
. Значения 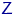 мы либо задаем, либо наблюдаем. Обозначим через
мы либо задаем, либо наблюдаем. Обозначим через 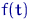 функцию, отражающую зависимость среднего значения
функцию, отражающую зависимость среднего значения 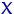 от значений
от значений 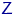 :
:
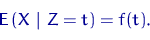
| (6) |
Функция 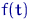 называется линией регрессии
называется линией регрессии 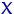 на
на 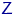 , а уравнение
, а уравнение  -- регрессионным уравнением. После
-- регрессионным уравнением. После 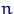 экспериментов, в которых
экспериментов, в которых 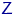 последовательно принимает значения
последовательно принимает значения  ,
,  ,
, 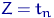 , получим значения наблюдаемой величины
, получим значения наблюдаемой величины 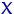 , равные
, равные 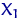 ,
,  ,
, 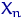 .
.
Обозначим через 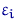 разницу
разницу
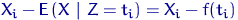
между наблюдаемой в 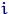 -м эксперименте случайной величиной и ее математическим ожиданием.
-м эксперименте случайной величиной и ее математическим ожиданием.
Итак, 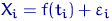 ,
,  , где
, где 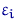 — ошибки наблюдения, равные в точности разнице между реальным и усредненным значением случайной величины
— ошибки наблюдения, равные в точности разнице между реальным и усредненным значением случайной величины 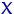 при значении
при значении  . Про совместное распределение
. Про совместное распределение 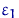 ,
,  ,
, 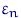 обычно что-либо известно или предполагается: например, что вектор ошибок
обычно что-либо известно или предполагается: например, что вектор ошибок 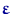 состоит из независимых и одинаково нормально распределенных случайных величин с нулевым средним.
состоит из независимых и одинаково нормально распределенных случайных величин с нулевым средним.
Нулевое среднее тут необходимо:
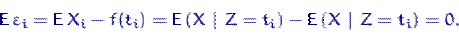
Требуется по значениям 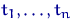 и
и 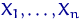 оценить как можно точнее функцию
оценить как можно точнее функцию 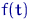 . Величины
. Величины 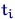 не являются случайными, так что вся случайность сосредоточена в неизвестных ошибках
не являются случайными, так что вся случайность сосредоточена в неизвестных ошибках 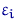 и в наблюдаемых
и в наблюдаемых 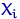 .
.
|
|
|
Но пытаться в классе всех возможных функций восстанавливать 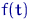 по «наилучшим оценкам» для
по «наилучшим оценкам» для 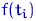 довольно глупо — наиболее точными приближениями к
довольно глупо — наиболее точными приближениями к 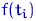 оказываются
оказываются 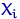 , и функция
, и функция 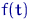 будет просто ломаной, построенной по точкам
будет просто ломаной, построенной по точкам 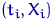 . Поэтому сначала заранее определяют вид функции
. Поэтому сначала заранее определяют вид функции 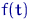 . Часто предполагают, что
. Часто предполагают, что 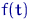 есть полином (редко больше третьей или четвертой степени) с неизвестными коэффициентами. Будем пока предполагать, что функция
есть полином (редко больше третьей или четвертой степени) с неизвестными коэффициентами. Будем пока предполагать, что функция 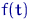 полностью определяется неизвестными параметрами
полностью определяется неизвестными параметрами 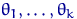 .
.
 2014-02-02
2014-02-02 269
269








