Основные понятия теории вероятностей. Як виробити ці критерії? Як їх використати під час переговорів?

Як виробити ці критерії? Як їх використати під час переговорів?

Як мінімум, вони повинні бути незалежними від бажань чи позицій опонентів. В ідеалі вони повинні бути виправданими і практичними.

Об’єктивні критерії повинні, хоча б в теорії, бути такими для обох сторін. (Право на самовизначення: спочатку добиваються для себе, потім відмовляють у цьому меншинам.)

Для прийняття незалежного від бажань сторін рішення можна покладатися або на чесні критерії або чесні процедури. Одна з найбільш відомих процедур – це один ділить, другий вибирає. Варіації – вирішувати/пропонувати по черзі, запросити ще когось до вирішення

n Визначивши певні об’єктивні критерії і процедури, треба вміти їх застосовувати. Тут автори пропонують три принципи:

1) Визначайте кожне питання як спільний пошук об’єктивних критеріїв.

Уявіть собі, що ви купуєте будинок. Хочете його за меншу ціну, а продавець за вищу. Починайте обговорення ціни приблизно так: “Ви хочете одну ціну, а я іншу. Давайте подивимось, яка буде реальна ціна будинку.” (Які ціни на такі будинки в регіоні, скільки років будинку, як оцінює будинок бюро інвентаризації).

Якщо продавець визначає вам ціну 20 тис.доларів. Запитайте, як вивизначили цю ціну?

2) Будьте розсудливими.

Твердження про те, що рішення повинно прийматися на основі об’єктивних критеріїв, не означає, що ці критерії повинні задовільняти ваші інтереси. Тому враховуйте аргументи вашого опонента і намагайтеся погодити з ним критерії.

3 )Не піддавайтесь тиску.

Тиск опонента може мати різні форми: підкуп, погрози, шантаж, маніпуляції або просто відмова брати участь в переговорах. У всіх цих випадках

принципова відповідь повинна бути та сама: запитайте їхні міркування про ціну, терміни тощо, запропонуйте об’єктивні критерії і не погоджуйтесь на угоду ні на яких інших умовах, крім цих.

Хто переможе, важко сказати, але перевага буде на вашому боці, бо ви відкриті для обговорення на об’єктивних умовах і ви дискутуєте не з приводу позицій, а з приводу об’єктивних стандартів.

Опытом называется всякое осуществление определенных условий или действий, при которых наблюдается изучаемое случайное явление. Примеры опытов: подбрасывание иг­ральной кости, выстрел по мишени, измерение физической величины. Событие – качест­венная характеристика результата опыта. Например, при бросании игральной кости – вы­падение единицы или двойки; попадание в мишень при стрельбе; в случае измерения – его результат составляет столько-то единиц.

Событие называется достоверным, если оно обязательно происходит в результате опыта. Событие называется невозможным, если оно не может произойти в результате данного опыта. В опыте с игральной костью достоверное событие – выпадение любой цифры – от 1 до 6; невозможное событие – появление семерки. Событие, которое в результате опыта может появиться, а может - нет, называется случайным.

Рассмотрим повторяющиеся опыты, выполняемые в одинаковых условиях. Пусть после выполнения n опытов некоторое событие А произошло m раз. Тогда под частотой этого события P*(A) понимают отношение:

P*(A) = m/n.

Вероятностью P(A) некоторого случайного события А называется число, характери­зующее частоту этого события при большом числе опытов. Из этих определений следует, что вероятность – величина неотрицательная и ограниченная областью 0£ P(A) £ 1,0.

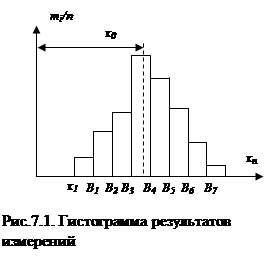В некоторых простых случаях числовое значение вероятности события может быть оценено до опыта. Например, при подбрасывании симметричной монеты выпадение герба или цифры равновероятны и равны 0,5. При подбрасывании симметричной игральной кос­ти равновероятно выпадение любой цифры из допустимых 1, 2,…,6. Поэтому вероятности выпадения каждой из цифр одинаковы и равны 1/6. Однако, на практике такой анализ со­бытия затруднен и при определении вероятности того или иного события руководствуют­ся экспериментальными данными, либо выполняя большое число опытов, либо используют такие опыты, в которых появление события зависит от множества факторов. Пусть произведен ряд изме­рений некоторой величины Х. Пересортируем результаты измерений в порядке их возрастания: х₁< х₂< ….<х_n-1<x_n. Таким образом, область возможных значений измеряемой величины находится в пределах от минимального х₁ до максимального x_n. Разделим эту область на несколько (например, на восемь) интервалов. Границы интервалов обозначим В₁, В₂, … В₇. Подсчитаем относительное количество m_i/n ре­зультатов измерений, попадающих в i-тый интервал, и по результатам расчетов построим ступенчатую кривую, называемую гисто­граммой. Типичный вид подобной гистограммы показан на рис.7.1. Видны основные свой­ства результатов измерений:

· чем ближе результат измерения к истинному значению х₀, тем чаще он встречается;

· отклонения результата измерения одинаковой величины, но разные по знаку встречаются одинаково часто.

Если увеличивать число измерений одной и той же величины, одновременно увели­чивая число интервалов деления возможных значений результата измерения, то ступенча­тый характер гистограммы сглаживается и в пределе она превращается в непрерывную плавную функцию (рис.7.2). Такая функция называется функцией распределения плотности вероятности f(x). Интеграл от функции плотности вероятности, взятый в некоторых пределах от х₁ до х₂, равен вероятности того, что случайная величина х примет значение х₁<x<x₂:

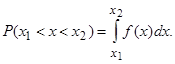
Графически этот интеграл представля­ет собой площадь под кривой f(x), ограни­ченную ординатами х=х₁ и х=х₂. Функция распределения плотности вероятности является наиболее полным описанием случайной величины. Часто используют более простые числовые характеристики случайной величины:

математическое ожидание m_x

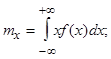
дисперсия D_x

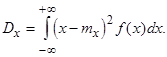
Математическое ожидание m_x представляет собой наиболее вероятное значение случайной величины х. Дисперсия D_x характеризует степень разброса случайной величины х относительно математического ожидания вдоль числовой оси. Размерность дисперсии – квадрат размерности случайной величины х, что не всегда удобно. Поэтому употребляют среднее квадратическое отклонение случайной величины, равное квадратному корню из дисперсии:

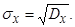
Если имеется случайная величина х с математическим отклонением m_x, то случайная величина у = х - m_x называется центрированной случайной величиной. Математическое ожидание центрированной случайной величины равно нулю.

Чаще всего используют нормальное распределение вероятности, плотность которого описывается формулой:

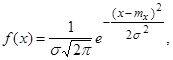
где m_x – математическое ожидание случайной величины х,

s - среднее квадратическое отклонение случайной величины х.

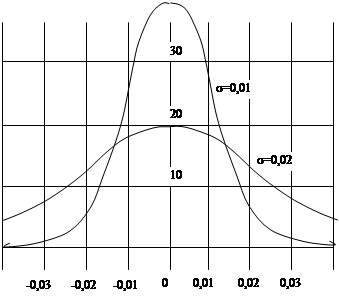
Кривые нормального распределения для двух значений s показаны на рис. 7.2. Видно, что параметр s определяет степень разброса случайной величины: чем меньше s, тем более компактно распределена случайная величина на числовой оси, тем больше вероятность результатов измерений, близких к действительному значению измеряемой величины. Таким образом,среднее квадратическое отклонение s случайной величины х может служить характеристикой точности измерения.