РАЗЛОЖЕНИЕ ПЛОСКОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА НА ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ
Любое движение твердого тела, в том числе и движение плоской фигуры в ее плоскости, бесчисленным множеством способов можно разложить на два движения, одно из которых переносное, а другое – относительное. В частности, движение плоской фигуры в ее плоскости относительно системы координат O1x1y1, расположенной в той же плоскости (рис. 25), можно разложить на переносное и относительное движения следующим образом. Примем за переносное движение фигуры ее движение вместе с поступательно движущейся системой координат Ox’ 1 y’ 1, начало которой скреплено с точкой О фигуры, принятой за полюс. Тогда относительное движение фигуры будет по отношению к подвижной системе координат Ox’ 1 y’ 1 ращением вокруг подвижной оси, перпендикулярной плоской фигуре и проходящей через выбранный полюс О.
Применяя к плоскому движению теорему о сложении скоростей для какой-либо точки В фигуры, получаем
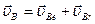 , (*)
, (*)
где 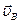 – абсолютная скорость точки В плоской фигуры относительно системы координат, по отношению к которой рассматривается движение фигуры;
– абсолютная скорость точки В плоской фигуры относительно системы координат, по отношению к которой рассматривается движение фигуры; 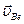 – скорость точки В от переносного поступательного движения фигуры вместе, например, с точкой А этой фигуры (рис. 26, а).
– скорость точки В от переносного поступательного движения фигуры вместе, например, с точкой А этой фигуры (рис. 26, а).
|
|
|
Так как за переносное движение выбрано поступательное
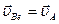
Скорость относительного движения, в случае когда оно является вращательным движением, равна
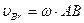
Эту относительную скорость можно выразить в виде векторного произведения:
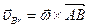 ,
,
где угловая скорость 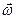 считается направленной по подвижной оси вращения.
считается направленной по подвижной оси вращения.
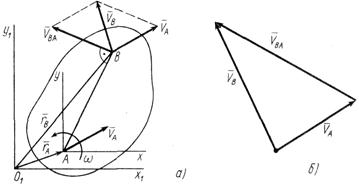
Рис. 26
Формулу (*) можно выразить в виде
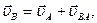
где
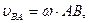
а вектор 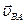 перпендикулярен отрезку АВ и направлен в сторону вращения плоской фигуры (рис.26, а).
перпендикулярен отрезку АВ и направлен в сторону вращения плоской фигуры (рис.26, а).
Таким образом, скорость какой-либо точки фигуры при её плоском движении равна векторной сумме скорости полюса и относительной скорости этой точки от вращения фигуры вокруг полюса. Вышеприведенная формула выражает зависимость между скоростями двух любых точек тела при плоском движении в любой момент времени. Эту формулу, устанавливающую зависимость скоростей двух точек плоской фигуры, можно получить непосредственным дифференцированием по времени векторного равенства
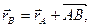
справедливого для любого момента времени (см. рис. 26, а).
При дифференцировании векторов учитываем их изменения относительно основной, неподвижной, системы координат 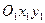 , т.е. вычисляем полные производные от этих векторов. Имеем
, т.е. вычисляем полные производные от этих векторов. Имеем
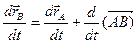 .
.
Очевидно, 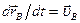 ,
, 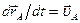 - скорости точек В и А. Вектор
- скорости точек В и А. Вектор 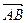 соединяет две точки плоской фигуры и, следовательно, не изменяется по модулю при движении плоской фигуры. Производную по времени от такого вектора как вектора постоянного модуля по скалярному аргументу можно выразить в форме
соединяет две точки плоской фигуры и, следовательно, не изменяется по модулю при движении плоской фигуры. Производную по времени от такого вектора как вектора постоянного модуля по скалярному аргументу можно выразить в форме
|
|
|
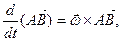
где 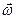 - вектор угловой скорости вращения
- вектор угловой скорости вращения 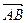 , а следовательно. и плоской фигуры, с которой скреплён вектор
, а следовательно. и плоской фигуры, с которой скреплён вектор 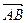 .
.
Окончательно имеем
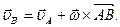
Если ввести обозначение 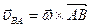 , то
, то
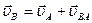 .
.
 2014-02-17
2014-02-17 750
750








