2014-02-09
1087
Общее уравнение линии 2-го порядка
В аффинной системе координат общее уравнение линии 2-го порядка имеет вид:
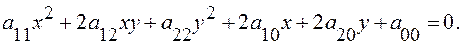(11)
Коэффициенты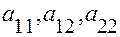 
не равны) одновременно.
Приведем уравнение (11) к каноническому виду. Для этого будем рассматривать его в ортонормированном репере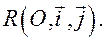 
Часть 1. Преобразуем систему координат поворотом на угол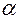 
вокруг начала.
Запишем формулы преобразования:
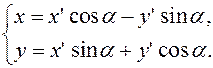(12)
Подставим (12) в (11):
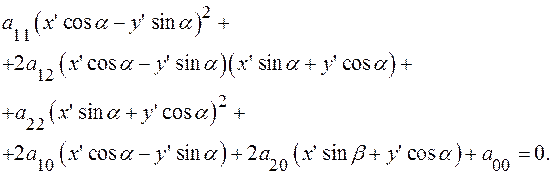
В новых переменных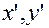 
уравнение запишем так:
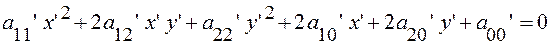
(11’)
где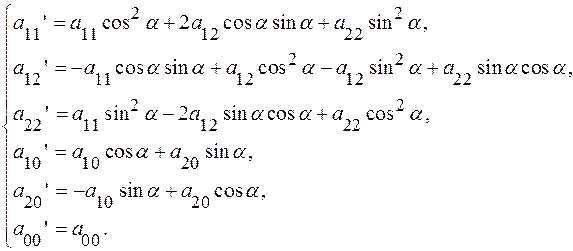
(13)
1/ Если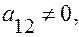 
то подберем угол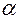так, чтобы уравнение (11’) не содержало члена с произведением 
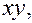то есть чтобы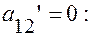 
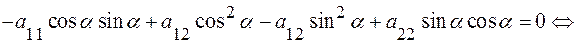
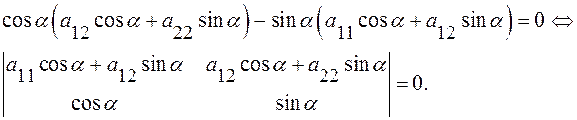Определитель равен) тогда и только тогда, когда его строки пропорциональны:
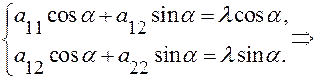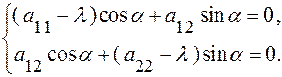(14’)
(14)
Система (14) однородных уравнений имеет нетривиальное решение, если её определитель равен 0:
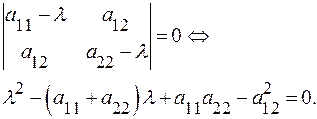(15)
Опр. Уравнение (15) называется характеристическим уравнением линии 2-го порядка.
Покажем, что его коэффициенты не зависят от выбора ортонормированного репера.
Из (13):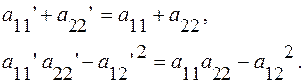 
2.По предположению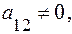 
поэтому дискриминант уравнения (15):
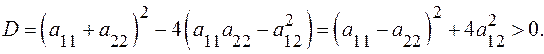
Значит, характеристическое уравнение (15) всегда имеет действительные и различные корн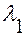и 
и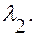 
Из (14) следует:
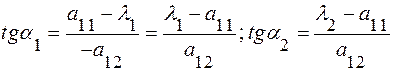(16)
По формулам Виета: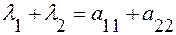 
и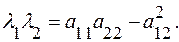 
Тогда
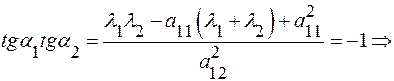
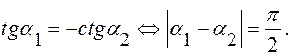
Любой из углов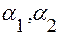 
можно взять за угол поворота осей, при этом исчезает член с произведением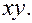 
Найдем коэффициенты уравнения (11’) из системы (13), учитывая(14’).
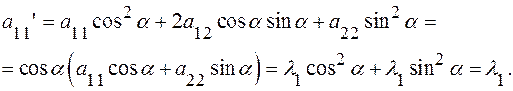
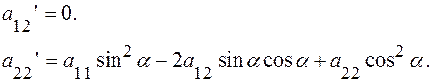
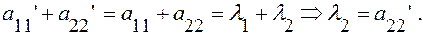
Итак, для любой линии 2-го порядка, заданной в ортонормированном репере уравнением (11), существует ортонормированный репер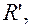 
в котором её уравнение имеет вид 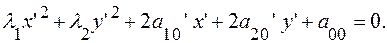(17):
(17)
Пример. Приведите к каноническому виду уравнение:
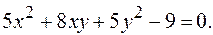
∆ 1.Запишем характеристическое уравнение данной кривой и найдем его корни.
(15)
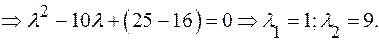
2. В новой системе координат уравнение имеет вид:
(17)
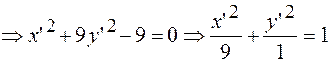- эллипс.
3. Запишем формулы преобразования координат.
(16)
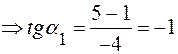или 
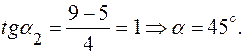
(12)
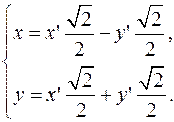
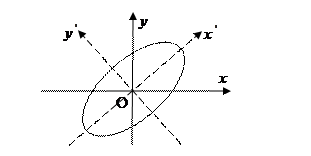
4. Чертеж.
Часть 2. Исследуем уравнение (17):
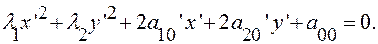
Случай 1.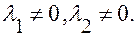 
Преобразуем уравнение (17), выделяя полные квадраты.
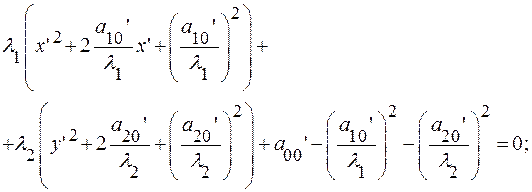
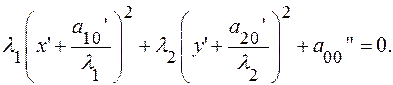(18)
Перенесем начало координат в точку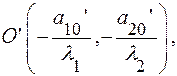 
то есть выполним преобразование «перенос начала координат»:
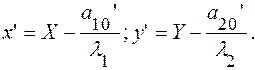
Уравнение (18) примет вид:
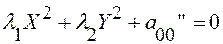(19)
а) 
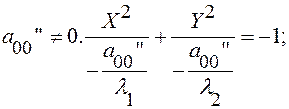б)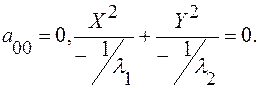
Вывод. Если корни характеристического уравнения не равны 0, то линия 2-го порядка является линией одного из следующих видов:
| № |
| 
| 
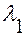
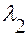
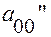
| Каноническое уравнение | Название линии |
| 1. | + - | + - | - + |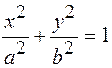 
| Эллипс |
| 2. | + - | + - | + - |
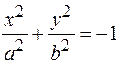
| Мнимый эллипс |
| 3. | + - | + - |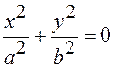 
| Точка 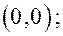 пара мнимых прямых, пересека-
ющихся в этой точке
| |
| 4. | + - | - + |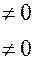 
| 
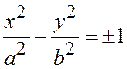
| Гипербола |
| 5. | + - | - + |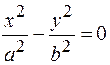 
| Пара пересекающихся прямых |
Случай 2.
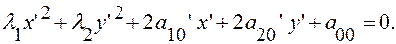(17)
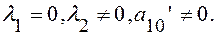
(17) 
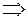
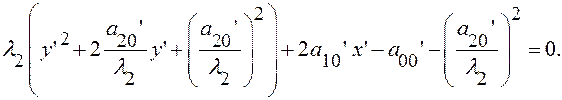
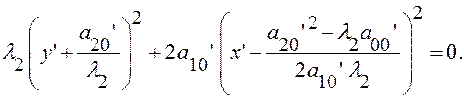
Перенос начала в точку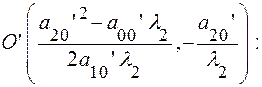 
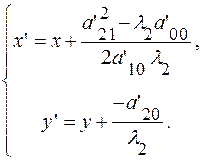
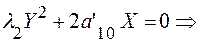
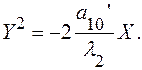
В случае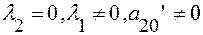 
получим уравнение параболы:
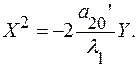
Случай 3.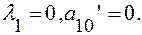 
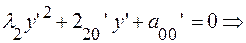
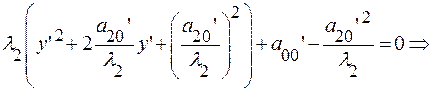
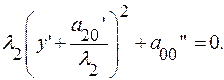Параллельный перенос в точку 
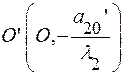преобразует уравнение: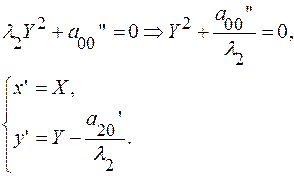 
а)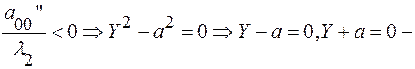 
две
действительные параллельные прямые.
б)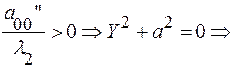 
две мнимые параллельные прямые.
в)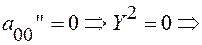 
2 совпавшие прямые.
Вывод: уравнение (11) определяет одну из 9-ти линий:
1) эллипс,
2) гипербола,
3) парабола,
4) мнимый эллипс,
5) пара пересекающихся прямых,
6) пара параллельных прямых,
7) пара совпавших прямых,
8) пара мнимых прямых, пересекающихся в действительной точке,
9) пара мнимых параллельных прямых.
