Особые точки. Особые решения

Теорема о существовании и единственности решения (вторая формулировка). Если в уравнении

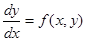(1)

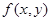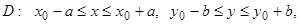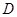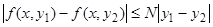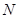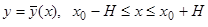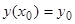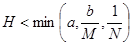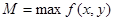функция непрерывна в прямоугольнике и удовлетворяет в условию Липшица: , где — постоянная, то существует единственное решение уравнения (1), удовлетворяющее условию , где , в .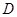

Условие Липшица может быть заменено несколько более грубым, но зато обычно легко проверяемым условием существования ограниченной по модулю частной производной 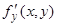в области : .

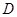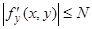Теперь рассмотрим точки 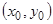, в окрестности которых решения уравнения (1), удовлетворяющего условию 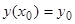, не существует или решение существует, но не единственно. Такие точки называются особыми точками.

Кривая, состоящая сплошь из особых точек, называется особой. Если график некоторого решения сплошь состоит из особых точек, то решение называется особым.

Для нахождения особых точек или особых кривых надо прежде всего найти множество точек, в которых нарушены условия теоремы о существовании и единственности решения, так как только среди таких точек могут быть особые. Конечно, не каждая точка, в которой нарушены условия теоремы о существовании и единственности решения, обязательно является особой, так как условия этой теоремы достаточны для существования и единственности решения, но они не являются необходимыми.

Первое условие теоремы о существовании и единственности решения нарушается в точках разрыва функции 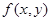, причем если при приближении по любому пути к некоторой изолированной точке разрыва 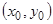функция 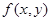неограниченно возрастает по модулю, то в тех задачах, в которых переменные 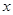и 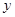равноправны, как мы говорили ранее, уравнение (1) должно быть заменено уравнением 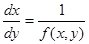, для которого правая часть уже непрерывна в точке 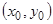, если считать .

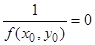Следовательно, в задачах, в которых переменные 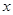и 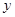равноправны, первое условие теоремы существования и единственности нарушается в тех точках, в которых и функция 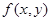и 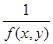разрывны.

Особенно часто приходится рассматривать уравнения вида

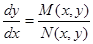, (2)

где функци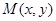и и 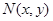непрерывны. В этом случае функция 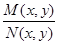и 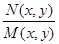будут одновременно разрывны лишь в тех точках 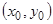, в которых 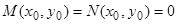и не существует пределов 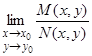и .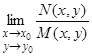

Рассмотрим несколько типичных особых точек уравнения (2).

Пример. .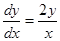

Правые части данного уравнения и уравнения 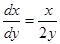разрывны в точке 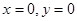. Интегрируя уравнение, получим 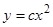— семейство парабол и 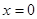. В начале координат — особая точка, называемая узлом.

Пример. .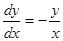

Правые части данного уравнения и уравнения 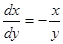разрывны в точке 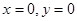. Интегрируя уравнение, получаем 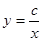— семейство гипербол и прямую 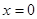. В начале координат — особая точка, называемая седлом.

Пример. .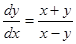

Правые части данного уравнения и уравнения 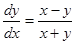разрывны в точке 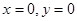. Интегрируя рассматриваемое однородное уравнение, получим 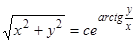, или в полярных координатах 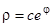— логаримические спирали. Особая точка такого типа называется фокусом.

Пример. .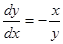

Правые части данного уравнения и уравнения 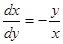разрывны в точке 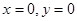. Интегрируя уравнение, получаем 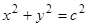— семейство окружностей с центром в начале координат. Особая точка такого типа, т.е. особая точка, окрестность которой заполнена семейством замкнутых интегральных кривых, называется центром. В этом примере не существует решения, удовлетворяющего условию .

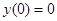Второе условие теоремы о существовании и единственности решения — условие Липшица, или более грубое условие, требующее существования ограниченно частной производной 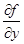, чаще всего нарушается в точках, при приближении к которым 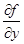неограниченно возрастает, т.е. в точках, в которых .

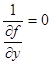Уравнение 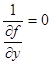, вообще говоря, определяет некоторую кривую, в точках которой может быть нарушена единственность. Если в точках этой кривой единственность нарушена, то кривая будет особой. Если, кроме того, эта кривая окажется интегральной, то получим особую интегральную кривую.

Возможно, что кривая 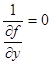имеет несколько ветвей, тогда для каждой ветви надо решить вопрос о том, будет ли эта ветвь особой кривой и будет ли она интегральной кривой.

Пример. Имеет ли уравнение 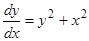особое решение?

Условия теоремы существования и единственности выполнены в окрестности любой точки, следовательно, особого решения нет.

Пример. Имеет ли уравнение 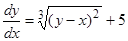особое решение?

Правая часть непрерывна, но частная производная 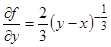неограниченно возрастает при приближении к прямой 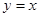, следовательно, на этой прямой может нарушиться единственность. Но функция 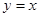не удовлетворяет рассматриваемому уравнению, следовательно, особого решения нет.

Пример. Имеет ли уравнение 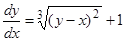особое решение?

Как и в предыдущем примере, частная производная неограниченно возрастает при приближении к прямой 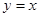, но на этот раз функция 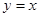удовлетворяет данному уравнению. Остается выяснить, нарушена ли единственность в точках этой прямой. Заменой переменных 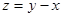приводим исходное уравнение к уравнению с разделяющимися переменными, после чего находим решение: 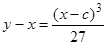. Кривые этого семейства проходят через точки графика решения 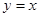. Следовательно, в каждой точке прямой 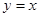единственность нарушена и функция 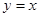является особым решением.

Этот пример показывает, что одной непрерывности правой части в уравнении 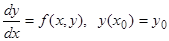, недостаточно для единственности решения основной начальной задачи, однако можно доказать, что существование решения при этом уже обеспечивается.