2014-02-18
922
 |
Течение идеальной несжимаемой жидкости в пределах трубки тока описывается уравнением Бернулли.
Выделим объем жидкости, которая в некоторый момент времени t заполняет участок, ограниченный сечениями S 1 и S 2 (рис. 6.2). Давление в сечении S 1 равно P 1, а в сечении S 2 - P 2.
Если течение стационарное, то объем жидкости к моменту времени t+ Δ t переместится и будет заключен между сечениям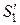и 
и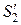 
. Промежуток Δ t выберем настолько малым, что скорости течения жидкости в пределах объема трубки тока, ограниченного сечениями S 1 и 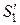, а также S 2 и 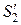,, можно считать постоянными.
Определим изменение полной механической энергии за малый промежуток времени D t. За это время масса жидкости, заключенная между сечениями S 1 и 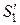втекает в рассматриваемую область, а масса, заключенная между сечениями S 2 и 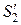вытекает из нее. Для идеальной жидкости изменение полной энергии D W равно разности полных энергий вытекающей и втекающей масс, или
D W = (T + U)2 – (T + U)1 , (6.4)
где T – кинетическая энергия выделенного объема жидкости, U - потенциальная энергия этого объема. Втекающая в выделенный объем и вытекающая из этого объема массы жидкости D m равны, поэтому формулу (6.4) можно переписать через массу:
|
|
|
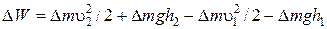, (6.4)
Где υ2 и υ1 – скорости объема в сечениях S 2 и S 1 , h1 и h2 – высота сечений S 1 и S 2 относительно некоторого уровня, соответственно. Изменение полной механической энергии равно работе A внешних сил по перемещению массы D m
D W = A.
На данный объем жидкости
действуют силы F 1 = p1 S 1 в сечении S 1, F 2 = p2 S 2 в сечении S 2 и силы давления, приложенные к боковой поверхности трубки тока.
Сила F 1 совершает работу A 1 по перемещению втекающей массы на пути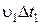 
.
При перемещении вытекающей массы совершается работа A 2 против силы F 2 на пути u2 D t.
Работа сил давления, приложенных к боковой поверхности трубки тока, равна нулю, так как эти силы направлены перпендикулярно к направлению течения жидкости.
Поэтому: A1= F 1 u1 D t, A 2= – F 2 u2 D t. Знак минус означает, что сила F 2 направлена против движения жидкости. Искомая работа A = A 1 + A 2 = F 1 u1 D t – F 2 u2 D t. Используя выражения для силы через давления, получим
A = p 1 S 1 u1 D t – p 2 S 2 u2 D t,
где S 1 u1 D t = S 2 u2 D t = D V - объем рассматриваемых масс. Поэтому
A = p 1 D V – p 2 D V. (6.5)
Приравнивая (6.4) и (6.5), получим
.
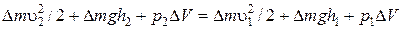Выразив Δ m через плотность r (Δ m = rD V), получим
.
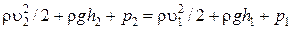Поскольку сечения S 1 и S 2 выбраны произвольно, то в общем случае можно записать:
ru2/2 + r gh + p = const. (6.6)
Соотношение (6.6) представляет собой уравнение Бернулли. Для горизонтальной трубки тока уравнение Бернулли имеет вид
ru2/2 + p = const. (6.7)
При отсутствии течения (υ=0) из (6.7)получим p = const. Это давление в выражениях (6.6) и (6.7) p называют статическим.
|
|
|
Величина ru2/2 - динамическое давление,
rgh ‑ гидростатическое давление.
Можно показать, что в случае установившегося течения константа в правой части уравнения (6.6) одинакова для всех трубок тока, т. е. что уравнение Бернулли справедливо для всего потока. ограниченного стенками трубы.
Из уравнений Бернулли и неразрывности следует, что в местах сужения трубопровода (или уменьшения сечения трубки тока) скорость течения жидкости возрастает, а давление понижается.
Пример 6.1. Применение уравнения Бернулли для расчета скорости истечения жидкости сквозь малое отверстие в стенке или дне сосуда. Рассмотрим сосуд, заполненный идеальной жидкостью. В боковой стенке его на глубине Н ниже уровня жидкости проделано малое отверстие (рис. 6.3).
 |
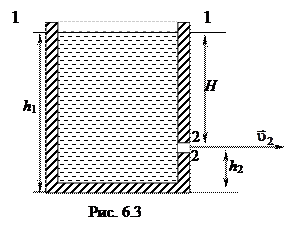Для двух сечений 1‑1 и 2‑2 запишем уравнение Бернулли
.
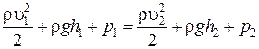В этой формуле p1 = p2 ‑ атмосферное давление. Тогда
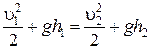. (6.8)
Из уравнения неразрывности
,
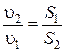где S 1 и S 2 ‑ площади поперечных сечений сосуда и отверстия. Поскольку S 1 >> S 2, то членом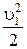 
в левой части уравнения (6.8) можно пренебречь. Тогда
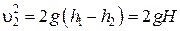и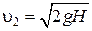 
. (6.9)
Полученное уравнение имеет название формулы Торричелли. Из нее видно, что частицы жидкости, выходя из отверстия, имеют такую же скорость, какую они приобрели бы, свободно падая с высоты Н.
