Следствия из преобразований Лоренца

Относительность одновременности

Пусть в системе 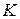в точках с координатам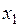и и 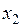в моменты времен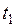и и 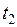происходят два события. В системе 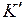им соответствуют координаты 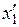и 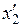и моменты 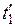и 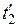. Если события в системе 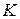происходят в одной точке (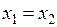) и являются одновременными (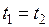), то, согласно преобразованиям Лоренца (5.4)

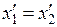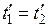, , (5.5)

т.е. эти события являются одновременными и пространственно совпадающими для любой инерциальной системы отсчета.

Если события в системе 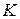пространственно разобщены (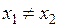), но одновременны (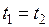), то в системе 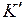, согласно преобразованиям Лоренца (5.4)

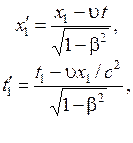
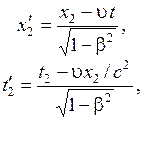(5.6)

Из (5.6) следует, что 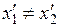и 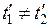. Таким образом, в системе 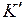эти события, оставаясь пространственно разобщенными, оказываются и неодновременными.

Длительность событий в разных системах отсчета

Пусть в некоторой точке (с координатой 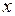), покоящейся относительно системы K, происходит событие, длительность которого (разность показаний часов в конце и начале события) 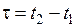, где индексы 1 и 2 соответствуют началу и концу события. Длительность этого же события в системе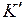

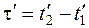, (5.7)

где

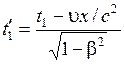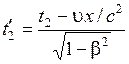, . (5.8)

Подставив (5.8) в (5.7), получаем

,

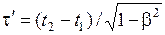или

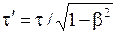. (5.9)

Отметим, что 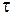< 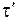, т. е. длительность события, происходящего в некоторой точке, наименьшая в той инерциальной системе отсчета, относительно которой эта точка неподвижна. Следовательно, часы, движущиеся относительно инерциальной системы отсчета, идут медленнее покоящихся часов, т.е. ход часов замедляется в системе отсчета, относительно которой часы движутся.

Длина тел в разных системах отсчета

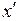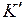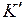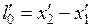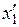Рассмотрим стержень, расположенный вдоль оси и покоящийся относительно системы . Длина стержня в системе будет , где и 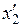– не изменяющиеся со временем 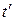координаты начала и конца стержня, индекс ноль показывает, что в системе 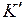стержень покоится. Определим длину этого стержня в системе K, относительно которой он движется со скоростью .

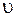Для этого необходимо измерить координаты его концов 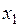и 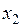в системе K в один и тот же момент времени t. Их разность 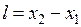и даст длину стержня в системе K:

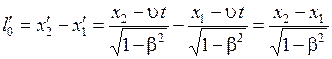, (5.10)

т. е.

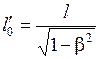. (5.11)

Размер тела, движущегося относительно инерциальной системы отсчета, уменьшается в направлении движении в 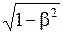раз, т. е. лоренцево сокращение длинытем больше, чем больше скорость движения. При этом поперечные размеры тела не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчета.

Релятивистский закон сложения скоростей

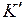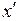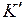Пусть материальная точка движется в системе вдоль оси , а движется относительно K со скоростью u (оси x и 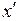совпадают), тогда из (5.4) получим

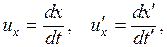(5.12)

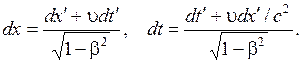(5.13)

Подставляя (5.13) в (5.12), получим релятивистский закон сложения скоростей:

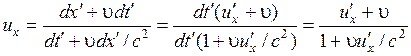. (5.14)

Аналогично получим обратные преобразования

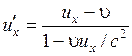. (5.15)

Если скорости 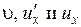малы по сравнению со скоростью света c, то эти формулы переходят в закон сложения скоростей в классической механике. Релятивистский закон сложения скоростей не противоречит второму постулату Эйнштейна. В самом деле, если 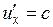, то 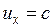. Если 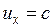, то 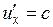, т. е. скорость с – предельная скорость, которую невозможно превысить.