Теорема Дедекінда (непрерівність множини дійсних чисел)

Сечение А / A ^¢ множества R вещественных чисел – это разбиение множества вещественных чисел на два непустых, непересекающихся подмножества, называемых классами (нижним А и верхним А ^¢) так что любое вещественное число из нижнего класса меньше любого числа из верхнего класса A ^¢:

1) A, А ^¢¹ F, 2) A È A ^¢=R, 3) A Ç A ^¢= Ф; 4) " aÎA "a^¢Î A ^¢ a < a ^¢.

Вещественное число a, производит сечение A | A ^¢ множества вещественных чисел R, если оно либо является наибольшим в нижнем классе a ₀=max A, либо наименьшим в верхнем классе a ₀=min A^¢.

Число наибольшее в нижнем классе А можно присоединить как наименьшее к верхнему классу А ^¢, исключив из нижнего, и наоборот; эта операция дает два сечения множества вещественных чисел, которые производятся одним и тем же вещественным число и отождествляются: если A | A^¢- сечение и

a₀= max A, то (A \{ a ₀})|(A ^¢È{ a ₀}- тоже сечения и a_{0 =}min(A ^¢È{a₀};

a₀ =min A ^¢, то (A È{ a ₀})(A ^¢\{ a ₀})- тоже сечение и a ₀=max (A È{ a ₀}).

Таким образом, вещественные числа есть классы эквивалентности сечений множества вещественных чисел.

Сечения А ½ А ^¢ множества вещественных чисел R у которых одновременно в нижнем классе А есть наибольший элемент, а в верхнем классе А ^¢ - наименьший не существуют.

3От противного. Если a ₀=max A и a ^¢₀=min A ^¢, то вставляя между ними, a ₀< a ^¢, вещественное число, скажем 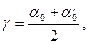a₀ < g <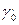придем к противоречию: g не может лежать в классе А т.к. g>a₀ =max A и g не может лежать в классе А ^¢ т. к. g <a^,₀=minA^¢

Не существуют также сечения A ½ A ^¢ вещественных чисел у которых одновременно в нижнем классе А нет наибольшего, а в верхнем классе А ^¢ - наименьшего числа. Иными словами имеет место теорема Дедекинда. Всевозможные приближения вещественными числами по недостатку к избытку однозначно определяют вещественное число.

Теорема Дедекинда о непрерывности множества вещественных чисел. Всякое сечение множества вещественных чисел производится некоторым вещественным числом:

" A | A ^¢ либо $aÎ R a₀=max A либо a₀ =min A^¢.

Очевидно, что всякое вещественное число a ₀ производит сечение A ½ A^¢ множества R вещественных чисел: нижний класс такого сечения это либо A ={x ÎR | x < a₀ }=]- µ,a [, либо A ={ xÎR | x £ a ₀}=]-µ, A ], а верхний - А ^¢={ xÎR | x ³a₀}=[a₀,+µ[, либо A ^¢={x ÎR | x > a ₀}=]a₀,+µ[ соответственно.

3Определим сечение множества рациональных чисел полагая A = Q ÇA и A ^¢= Q Ç A ^¢ Из определяющих свойств сечений множества вещественных чисел следуют для так определенных классов А и А ^¢ все определяющие свойства сечения A ½ A ^¢ множества рациональных чисел.

(Q Ç A)Ç ( Q Ç A ^¢)= Q Ç A Ç Q Ç A ^¢=(Q Ç Q)Ç(A Ç A ^¢)= Q ÇÆ=Æ,

(Q Ç A)È(Q Ç A ^¢)= Q Ç(A È A^¢)= Q Ç R = Q.

a ₀= A ½ A ^¢- сечение множества рациональных чисел – вещественное число a ₀. Поэтому, либо a,ÎA, либо a ₀ ÎA ^¢, т.к. A È A ^¢= R.

Если a ₀ ÎA и не является там наибольшим, то $ aÎA a ₀< a ×. Тогда вставляя между ними рациональное число r, a ₀< r < a приходим к противоречию: с одной стороны rÎA т.к. aÎA, а потому ÎA и любое число меньшее a; с другой стороны, rÎA^¢ т.к. r > a ₀ и так определено a ₀.

Случай a ₀ Î A^¢ рассматривается аналогично8

Всякое число входит в нижний (верхний) класс вместе со всеми числами меньшими (большими) его. Всякое числовое множество, которое не пустое, не совпадает с множеством всех чисел и вместе с любым числом содержит и все числа меньшие (большие) его, является нижним (верхним) классом некоторого сечения.

3" a ^¢ ÏM и " aÎM имеем a < a ^¢, т.к. иначе (т.е. если a¢ £ a) a ^¢ Î M. Остальные свойства сечений – это свойства дополнений множеств или оговорены в условии8