1. Классическое определение вероятности появления события A.
P(A) = 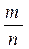 ;
;
m – число случаев, благоприятствующих появлению события A;
n – общее число случаев.
2. Теорема сложения вероятностей.
Вероятность появления одного из двух несовместных событий,
безразлично какого, равна сумме вероятностей этих событий, т.е.
P(A+B) = P(A) + P(B);
Если события совместны, то P(A+B) = P(A) + P(B) – P(A∙B);
Для трёх совместных событий
P(A+B+C) = P(A) + P(B) + P(C) + P(A∙B∙C) – P(A∙B) – P(A∙C) – P(B∙C).
3. Теорема умножения вероятностей.
Если события несовместны, то P(A∙B) = P(A) ∙ P(B);
P(A∙B·C) = P(A) ∙ P(B) · P(C);
Если события совместны, то P(A∙B) = P(A) ∙ PA(B);
P(A·B·C) = P(A) · PA(B) · PA·B(C);
4. Вероятность появления хотя бы одного события.
События A1, A2, …, An независимы, причем P(Ai) = pi. Тогда
вероятность появления хотя бы одного события равна
P = 1 – q1∙q2 … qn; где qi = 1 – pi; (i = 1, 2, …, n;)
Если все n событий имеют одинаковую вероятность, равную p, то
вероятность появления хотя бы одного события равна
P = 1 – qn; (q = 1 – p;)
5. Формула полной вероятности.
|
|
|
Вероятность события A, которое может наступить лишь при появлении
одного из несовместных событий (гипотез) H1, H2, …, Hn, образующих
полную группу, равна
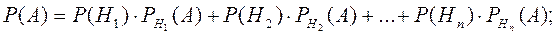
причём P(H1) + P(H2) + … + P(Hn) = 1.
6. Формула Бейеса.
Пусть событие A может наступить лишь при условии появления одного
из несовместных событий (гипотез) H1, H2, …, Hn, которые образуют
полную группу событий. Если событие A уже произошло, то вероят-
ности гипотез могут быть переоценены по формуле Бейеса
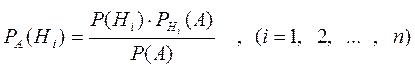 ,
,
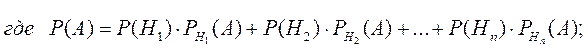
7. Повторение испытаний. Формула Бернулли.
Вероятность того, что в n независимых испытаниях, в каждом из
которых вероятность появления события равна p, событие наступит
ровно k раз (безразлично, в какой последовательности), равна
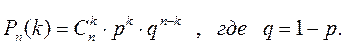
Вероятность того, что в n испытаниях событие наступит:
а) менее k раз Pn(0) + Pn(1) + … + Pn(k−1);
б) более k раз Pn(k+1) + Pn(k+2) + … + Pn(n);
в) не менее k раз Pn(k) + Pn(k+1) + … + Pn(n);
г) не более k раз Pn(0) + Pn(1) + … + Pn(k);
8. Наивероятнейшее число появления события в независимых испытаниях
Наивероятнейшее число k0 определяют из двойного неравенства
n·p – q ≤ k0 < n·p + q, (k0 – обязательно целое число)
причём:
а) если число (n·p – q) – дробное, то существует одно наивероятнейшее
число k0;
б) если число (n·p – q) – целое, то существует два наивероятнейших
числа, а именно: k0 и k0 + 1;
в) если число n·p – целое, то наивероятнейшее число k0 = n·p.
9. Производящая функция.
Пусть производится n независимых испытаний, причём в первом испы-
тании вероятность появление события A равна p1, во втором – p2, …,
в n – ом испытании – pn; вероятности непоявления события A соответ-
ственно равны q1, q2, …, qn; Pn(k) – вероятность появления события A
|
|
|
в n испытаниях ровно k раз.
Производящей функцией вероятностей Pn(k) называют функцию, опре-
деляемую равенством
φn(z) = (p1·z + q1)·(p2·z + q2) … (pn·z + qn);
Вероятность Pn(k) равна коэффициенту при zk в разложении функции
по степеням z (т.е. после раскрытия всех скобок).
10. Модой статистического ряда называется значение варианты, имеющей
наибольшую частоту.
11. Медианой упорядоченного статистического ряда называется значение
варианты, приходящееся на середину этого ряда.
Если число наблюдений нечётно, т.е. n = 2∙k – 1, то Me = xk;
Если число наблюдений чётно, т.е. n = 2∙k, то Me = 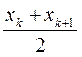 ;
;
******************************************************************
 2014-02-24
2014-02-24 418
418







