Радиус и интервал сходимости степенного ряда

Из теоремы Абеля следует, что если степенной ряд сходится, при некотором значении х₀, то этот ряд абсолютно сходится в промежутке изменения от -х₀ до х₀, (-х₀;х₀).

Если при некотором значении 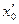ряд расходится, то он расходится для всех х удовлетворяющих неравенствам 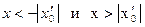, или 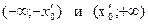- интервалы расходимости.

Определение: Интервал (-R;+R), внутри которого степенной ряд сходится, называется интервалом сходимости ряда. Половина интервала сходимости ряда называется радиусом сходимости.

(-R;+R)- интервал сходимости;

R- радиус сходимости.

На концах интервала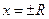ряд может сходиться и расходиться.

1. Если ряд (1) сходится в точке х=0, то R=0

2. Если ряд (1)сходится для любого х, то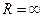

3. Если ряд (1) сходится в (-R;+R), то в x= -R и x= +R степенной ряд исследуется особо.

Укажем способ определения радиуса сходимости степенного ряда. 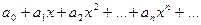(1)

Рассмотрим ряд, составленный из абсолютных величин его членов:

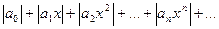(4)

Для определения сходимости ряда (4) применим признак Даламбера. Допустим, что существует предел:

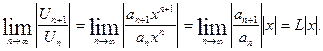
По признаку Даламбера ряд (4) сходится,

если 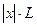<1, т.е. 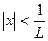и расходится если

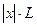>1, т.е. .

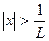Из предыдущего следует, что интервал сходимости 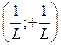обозначим 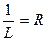, тогда 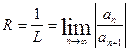(по Даламберу).

Аналогичным образом можно определить интервал сходимости по признаку Коши.

.

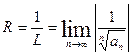Рассмотрим примеры: Определить интервалы сходимости степенных рядов

1)

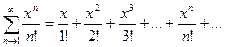
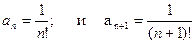
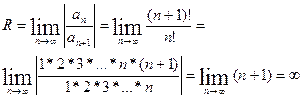
ряд сходится всюду .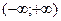

2)

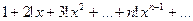
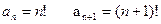
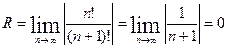
R=0. Ряд сходится в х=0.

3)

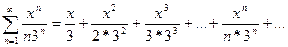
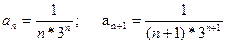
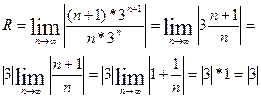
(-3;+3) - интервал сходимости. Исследуем ряд на концах:

х=-3.

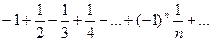условно сходится

х=3

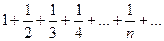расходится

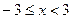или [-3;3) интервал сходимости.