Линия узлов

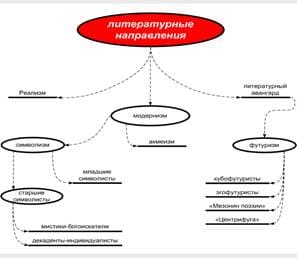
Описание ориентации с помощью углов Эйлера, самолетных (корабельных) углов.

Описание ориентации тела. Направляющие косинусы.

Как уже говорилось в параграфе (4.1.1), положение твердого тела можно описать вектором

положения какой-либо точки А, называемой полюсом, и ориентацией, которую удобно

описывать с помощью жестко связанной с телом тройки векторов. Для простоты возьмем

ортонормированную тройку векторов, которые в отсчетном положении обозначаются

, а в актуальном в момент времени. В качестве отсчетного

положения чаще всего удобно взять положение в момент времени, тогда,

но иногда в качестве отсчетного удобнее взять положение, которое тело никогда не занимало

в прошлом и, возможно, никогда не займет в будущем. Так, например, можно принять, что

- орты декартовой системы координат в используемой системе отсчета.

z

B

А y А

x

Разложим векторы по базису:

(k= 1,2,3) (4.7)

Скалярные произведения, равные косинусам углов между, называются

направляющими косинусами.

Принимая правило суммирования по повторяющимся индексам, вместо трех строчек (4.7),

в каждой из которых три слагаемых, можем написать короткую формулу

. (4.8)

При этом принимается соглашение, что по индексам, присутствующим в обеих частях

равенства (в данном случае это индекс) суммирование не производится, а равенство

повторяется «k» раз.

Имеется 9 направляющих косинусов, но только 3 из них являются независимыми, поскольку

между ними есть 6 уравнений связей

, где, напомним, называется символом Кронекера, или

(4.9)

В (4.9) символ «отфильтровал» в двойной сумме по индексам s и m только те

слагаемые, у которых s = m.

Знание направляющих косинусов полностью решает задачу описания движения, но выбрать три независимых и аналитически выразить через них остальные шесть невозможно, так как

система уравнений (4.9) нелинейная, поэтому в качестве трех параметров, задающих

ориентацию тела, обычно используются углы.

Рис. 4.3 Рис 4.4.

Традиционно углы Эйлера вводятся следующим образом. Переход из отсчетного

положения в актуальное осуществляется тремя поворотами (рис.4.3):

1. Поворот вокруг на угол прецессии При этом переходит в положение,(в).

2. Поворот вокруг на угол нутации. При этом,. (4.10)

4. Поворот вокруг на угол собственного (чистого) вращения

Для лучшего понимания на рис.4.4 изображен волчок и углы Эйлера, описывающие его

ориентацию.

Заметим, что можно доказать (догадаться трудно), что традиционная последовательность

поворотов (4.10) может быть заменена на последовательность поворотов на те же самые

углы вокруг неподвижных осей:

1. Поворот вокруг на угол собственного (чистого) вращения

2. Поворот вокруг на угол нутации.. (4.11)

4. Поворот вокруг на угол прецессии

Недостаток углов Эйлера в том, что при малом угле нутации углы и в линейном

приближении становятся неразличимы и входят в уравнения в виде суммы (+.

Этого недостатка лишены самолетные (корабельные) углы (рис.4.5).

Рис.4.5

Переход из отсчетного положения в актуальное можно осуществить

тремя поворотами (повернуть самостоятельно!) (рис.4.5):

1. Поворот вокруг на угол рысканья, при этом

2. Поворот вокруг на угол тангажа, при этом (4.12)

4.Поворот на угол крена вокруг

Выражение «можно осуществить» неслучайное; нетрудно понять, что возможны и другие

варианты, например, повороты вокруг фиксированных осей

1. Поворот вокруг на угол крена (рискуя сломать крылья)

2. Поворот вокруг на угол тангажа (подъем «носа») (4.13)

4. Поворот вокруг на угол рысканья

Впрочем, тождественность (4.12) и (4.13) также необходимо доказать.

4.2.4.Матрица поворота. Матрица спина. Вектор угловой скорости.

z В

В

В

А

А y

x Рис.4.6

Запишем очевидную векторную формулу для вектора положения какой-либо точки

(рис.4.6) в матричном виде. Найдем координаты вектора относительно

отсчетного базиса.

Разложим вектор по актуальному базису и введем «перенесенный» вектор

, координаты которого в отсчетном базисе равны координатам в актуальном;

иными словами - «повернутый» вместе с телом вектор (Рис.4.6).

Раскладывая векторы по отсчетному базису,получим

Введем матрицу поворота и столбцы,

Векторная формула в матричной записи имеет вид

(4.14)

1. Матрица поворота является ортогональной, т.е.

(4.15)

Доказательство этого утверждения – формула (4.9)

Вычисляя определитель произведения (4.15), получим а так как

в отсчетном положении, то (ортогональные матрицы с определителем,

равным (+1), называют собственно ортогональными или матрицами поворота). Матрица

поворота при умножении на векторы не изменяет ни длин векторов, ни углов между ними,

т.е. действительно их поворачивает.

2. Матрица поворота имеет один собственный (неподвижный) вектор, который задает

ось поворота. Иными словами, надо показать, что система уравнений, где

имеет единственное решение. Запишем систему в виде (. Определитель этой

однородной системы равен нулю, так как

,

следовательно, система имеет ненулевое решение. Предположив, что имеется два решения

, тут же придем к выводу, что перпендикулярный к ним также

является решением (углы между векторами не изменяются), а это значит, что

т.е. поворота нет..

В дальнейшем будем считать неподвижный вектор оси поворота единичным, а

положительное направление отсчета угла поворота согласованным с направлением

в соответствии с принятой ориентацией пространства (т.е. с конца положительный поворот

виден против часовой стрелки) (рис.4.7). Матрицу поворота будем обозначать

Матрица в ортонормированном базисе имеет вид

.

Рис.4.7

2. Дифференцируя (4.15), получим или, обозначив –

матрица спна (англ. to spin - вертеть). Таким образом, матрица спина

кососимметрическая:. Умножая справа на, получим формулу

Пуассона для матрицы поворота:

(4.16)

Мы подошли к самому трудному в рамках матричного описания моменту – определению

вектора угловой скорости.

Можно, разумеется, поступить стандартным (см., например, способом и написать:

«введем обозначения для элементов кососимметрической матрицы S по формуле

Если составить вектор, то результат умножения матрицы на

вектор может быть представлен в виде векторного произведения»

В приведенной цитате - вектор угловой скорости.

Дифференцируя (4.14), получим матричную запись основной формулы кинематики твердого

тела:

(4.17)

Матричный подход, будучи удобным для вычислений, очень мало подходит для анализа

и вывода соотношений; всякую формулу, написанную на векторном и тензорном языке, без

труда можно записать в матричном виде, а вот получить компактную и выразительную

формулу для описания какого-либо физического явления в матричном виде трудно.

Кроме того, не следует забывать, что элементы матрицы являются координатами

(компонентами) тензора в каком-либо базисе. Сам тензор не зависит от выбора базиса, а его

компоненты зависят. Для безошибочной записи в матричном виде необходимо, чтобы все

векторы и тензоры, входящие в выражение, были записаны в одном базисе, а это не всегда

удобно, поскольку разные тензоры имеют «простой» вид в разных базисах, поэтому нужно

пересчитывать матрицы с помощью матриц перехода.

4.2.4. Описание положения твердого тела с помощью тензора поворота.

Теорема Эйлера о тензоре поворота.

Положение тела описывается вектором положения какой-либо точки А и ориентацией

посредством тензора поворота, переводящим жестко связанную с телом тройку

векторов из отсчетного положения в актуальное: (рис.4.8)

z В

В

В

А

А y

x Рис.4.8

Раскладывая по отсчетному базису, будем иметь

, где называются

направляющими косинусами.

Теорема Эйлера. Произвольная ориентация твердого тела получается из отсчетной одним

поворотом на угол вокруг оси поворота.

В математическом виде теорема сводится к следующей теореме:

Теорема о представлении тензора поворота.

Тензор поворота, не равный, единственным образом можно представить в виде

+() (4.18)

Где -угол поворота, а единичный вектор задает прямую в пространстве, называемую осью поворота; положительное направление отсчета угла поворота согласовано с

направлением в соответствии с принятой ориентацией пространства, т.е. в

правоориентированном пространстве положительный поворот с конца виден против

часовой стрелки (рис. 4.7).

Доказательство.

Покажем, что существует единственный неподвижный вектор, т.е. уравнение

имеет единственное решение. Перепишем его в виде однородного

уравнения, которое имеет решение, только если определитель равен нулю,

что и следует из цепочки

Предполагая, что существуют два решения = и =, получим с помощью

тождества #2 (1.13), что и также является неподвижным вектором, что невозможно ().

Положим.

Подставляя эти выражения в тензор и, заменяя комбинации,

содержащие на независящие от их выбора выражения, придем к (4.18): +().

Можно доказать [2], что тензор поворота аналитически выражается через

произведение, называемым вектором поворота, поэтому в дальнейшем тензор поворота будем в необходимых случаях обозначать.

Представление (4.18) позволяет доказать весьма важную теорему:

Теорема. Если неподвижный вектор тензора), определяющий ось поворота, сам

получен поворотом, то. (4.19)

Иными словами: «тензор поворота с повернутой осью равен повернутому тензору»

Доказательство. Подставляя в (4.18), получим

,, и, полагая в тождестве #4 (1.16)

=.Таким образом,

+() +().

4.2.5. Тензор спина, вектор угловой скорости, формула Пуассона.

Дифференцируя по времени уравнение, получим

или, обозначив:,

то есть тензор =, называемый тензором спна - кососимметричный, поэтому он

может быть записан в виде (1.10):

, где (4.20)

называется вектором угловой скорости. Вектор задает ось вращения.

Исходя из представления Эйлера (4.18) можно прямым вычислением из (4.20) получить

(4.21)

Из (4.21) видно, что ось поворота и ось вращения совпадают только когда ось поворота

неподвижна (, тогда.

Умножив равенство справа скалярно на, получим формулу Пуассона

. (4.22)

4.2.6.Теорема о сложении угловых скоростей

Теорема. Если тензор поворота является композицией (произведением) поворотов

, то

, где - (4.23)

угловые скорости, соответствующие тензорам поворота.

Доказательство. Докажем сначала лемму:

Пусть – тензор поворота, – произвольный тензор, тогда

, (4.24)

«векторный инвариант повернутого тензора равен повернутому векторному инварианту».

Доказательство леммы немедленно следует из тождества #3 (1.15)

,в котором достаточно положить.

Впрочем, лемма имеет простой геометрический смысл. Примем в качестве одну диаду

(в лемму тензор входит линейно). Пусть векторы преобразуются

тензором в =, =, =. Поскольку тройка поворачивается как жесткая

система, то т.е.)=) или.

Вычисляя теперь тензор спина

+ =

и сопутствующие векторы левой и правой частей с помощью леммы (4.24) получим (4.23).

Упражнени е. Показать, что если,то

Дифференцируя (4.23), получим формулу сложения угловых ускорений

.

Заменив по формуле Пуассона =, будем иметь

= или, заметив, что

= (4.25)

Замечание.

Практически во всех учебниках не дается строгого определения угловой скорости, это понятие

остается затененным интуитивными соображениями (кроме случая фиксированной оси

поворота, когда). Доказываются «теоремы» о том, что «можно переносить вдоль

оси поворота», что угловые скорости можно складывать, если тело вращается вокруг

параллельных либо пересекающихся физических осей, но не рассматривается случай, когда оси не пересекаются и т.д. и т.п.

Теорема сложения угловых скоростей всегда приводится в виде. Очевидно, что под здесь понимается

4.2.7. Примеры вычисления вектора угловой скорости.

1. Углы Эйлера

Рис. 4.9 Рис 4.10.