Опр.: 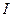 называется промежутком в
называется промежутком в 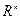 , если:
, если:
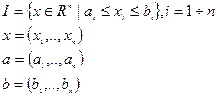
Опр.: Промежутку 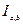 ставится в соответствие число
ставится в соответствие число 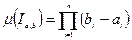 , которое называется мерой промежутка.
, которое называется мерой промежутка.
Лемма:
Мера промежутка удовлетворяет следующим свойствам:
1) она однородна:
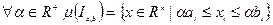
2) адитивность:
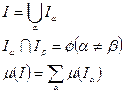
3) 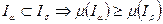
4) 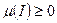
Разбиение промежутка
Опр.: 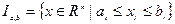
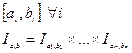
Прямое произведение разбиения сторон индуцирует разбиение всего промежутка.
Опр.: Отмеченные точки
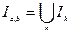 - разбиение промежутка
- разбиение промежутка
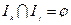
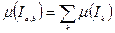
Для каждого промежутка 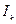 выбираем отмеченную точку
выбираем отмеченную точку 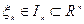
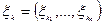
Опр.: Мелкость разбиения – число 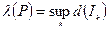
Опр.: Разбиение с отмеченными точками: 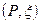
Интегральная сумма.
Опр.:
Пусть на интервале 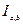 задана функция
задана функция 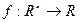 , тогда сумма
, тогда сумма 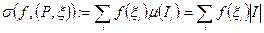 носит название «интегральная сумма».
носит название «интегральная сумма».
Опр.: 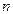 -мерный интеграл Римана:
-мерный интеграл Римана:
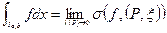
Если этот предел существует, тогда функция 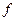 называется интегрируемой по Риману на
называется интегрируемой по Риману на 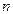 -мерном промежутке
-мерном промежутке 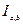 .
.
Класс функций, интегрируемых по Риману на промежутке 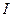 , обозначается
, обозначается 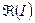 .
.
Кратный интеграл.
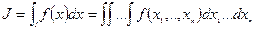
 2014-02-09
2014-02-09 1045
1045








