Найдем распределение тока в проводнике. Воспользуемся уравнениями Максвелла:
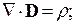 (17)
(17)
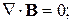 (18)
(18)
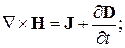 (19)
(19)
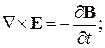 (20)
(20)
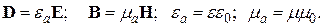 (21)
(21)
Запишем также уравнение закона Ома
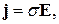 (22)
(22)
где постоянная 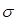 - удельная проводимость проводника. Плотность тока в уравнениях Максвелла может быть выражена с помощью этого уравнения через напряженность поля.
- удельная проводимость проводника. Плотность тока в уравнениях Максвелла может быть выражена с помощью этого уравнения через напряженность поля.
Совместное решение уравнений (19) и (17) позволит получить новое уравнение, содержащее только 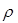 ; оно даст нам сведения об интересующей нас величине. Перепишем уравнение (19), исключив вектор плотности тока с помощью закона Ома:
; оно даст нам сведения об интересующей нас величине. Перепишем уравнение (19), исключив вектор плотности тока с помощью закона Ома:
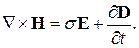 (23)
(23)
Возьмём теперь дивергенцию обеих частей уравнения (23) и учтём, что дивергенция ротора тождественно равна нулю, получим:
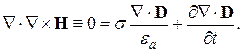
Дивергенция 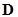 , согласно первому уравнению Максвелла, равна плотности заряда
, согласно первому уравнению Максвелла, равна плотности заряда 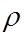 . Поэтому получим:
. Поэтому получим:
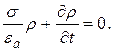 (24)
(24)
Решение уравнения (24)
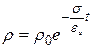 (25)
(25)
показывает, что плотность всякого заряда, который может появиться в проводнике, подчиняющемся закону Ома, должна уменьшаться экспоненциально, для хороших проводников — с очень большой скоростью. Любой заряд, помещённый внутри проводника, сразу же вышел бы на его поверхность; в соответствии с этим в уравнении Максвелла для стационарных состояний член, содержащий плотность заряда в проводнике, будет равен нулю, если только не придумаем средства непрерывно возобновлять внутри проводника свободные заряды. Таким образом, в проводниках
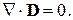 (26)
(26)
Если все величины пропорциональны 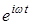 , уравнение (21) запишется в виде:
, уравнение (21) запишется в виде:
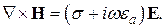 (27)
(27)
Токи смещения в любом относительно хорошем проводнике малы даже при наиболее высоких радиочастотах. Взяв синусоидальное колебание 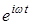 , сравним два члена уравнения (27) —
, сравним два члена уравнения (27) — 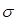 и
и 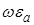 .
.
Рассмотрим случай когда 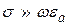 .
.
При радиочастотах, для всех проводников, кроме очень плохих, таких, например, как земля, токи смещения пренебрежимо малы по сравнению с токами проводимости. Остаётся
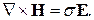 (28)
(28)
Возьмём ротор от обеих частей и развернём выражение для левой части:
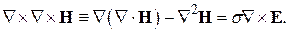 (29)
(29)
Подставив величины 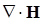 и
и 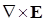 из уравнений Максвелла (18) и (20), получим:
из уравнений Максвелла (18) и (20), получим:
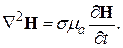 (30)
(30)
Подобное уравнение может быть получено так же и для 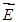 , если вместо (19) взять ротор обеих частей уравнения (20) и развернуть его, как было сделано выше:
, если вместо (19) взять ротор обеих частей уравнения (20) и развернуть его, как было сделано выше:
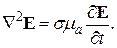 (31)
(31)
Так как 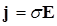 , то же уравнение может быть написано и для плотности тока
, то же уравнение может быть написано и для плотности тока
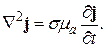 (32)
(32)
Если все величины изменяются синусоидально со временем, как 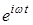 ,уравнение (32) запишется в виде
,уравнение (32) запишется в виде
При очень высоких частотах подавляющая часть тока сосредоточена в тонком слое у поверхности проводника. Но в таком случае кривизна самой поверхности несущественна, и становится возможным достаточно точно подсчитать распределение плотности тока, рассматривая малый элемент поверхности и пренебрегая его кривизной, т.е. принимая его за плоский проводник бесконечной толщины.
Примем для проводящего полупространства направление тока за ось z, а нормаль к поверхности за ось х и будем считать, что распределение остаётся неизменным вдоль осей y и z. Уравнение распределения плотности тока в этом случае будет:
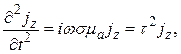 (34)
(34)
где 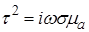 или
или 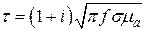 .
.
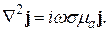 (33)
(33)
Полное решение этого уравнения имеет вид:
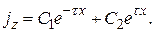 (35)
(35)
Постоянная 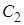 должна равняться нулю, иначе при
должна равняться нулю, иначе при 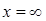 ток будет бесконечно велик, что невозможно.
ток будет бесконечно велик, что невозможно. 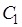 можно определить из граничного условия
можно определить из граничного условия 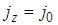 при
при 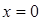 . Получаем:
. Получаем:
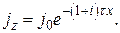 (36)
(36)
Введём новый параметр, который назовём глубиной проникновения:
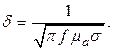 (37)
(37)
Если воспользоваться этим параметром, равенство перепишется в виде:
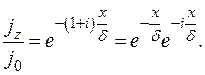 (38)
(38)
Из этой формулы следует, что величина плотности тока уменьшается экспоненциально с увеличением глубины, а 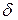 представляет значение глубины, на которой плотность тока падает до величины
представляет значение глубины, на которой плотность тока падает до величины 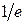 , т.е. примерно до 36,9% своего значения на поверхности. Фаза тока также меняется с увеличением глубины соответственно множителю
, т.е. примерно до 36,9% своего значения на поверхности. Фаза тока также меняется с увеличением глубины соответственно множителю 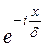 .
.
Для нахождения глубины проникновения монохроматической плоской волны в общем случае (с учётом двух слагаемых уравнения (27)) перепишем уравнение
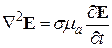 (39)
(39)
в виде:
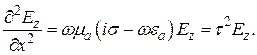 (40)
(40)
Здесь
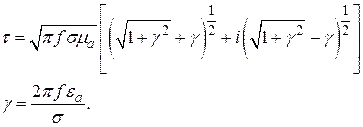 (41)
(41)
Глубина проникновения находится в виде
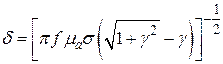 (42)
(42)
Уравнение (42) можно использовать при любых соотношениях между 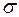 и
и 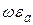
 2014-02-09
2014-02-09 1230
1230







