Обработка статистических данных при малом объёме выборки.
Методика обработки статистических данных в случае, когда выборка оказывается малой 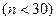 , имеет ряд особенностей, на которых мы и остановимся.
, имеет ряд особенностей, на которых мы и остановимся.
Пусть имеются семь оценок времени для выполнения одного и того же задания: 18; 24; 24; 28; 29; 32; 33 часа.
Найдём среднее время, гнеобходимое для выполнения задания.
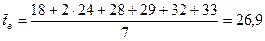 часа.
часа.
Так как объём выборки мал, то теряет смысл работа по составлению интервального ряда, построению кумулятивного графика.
Как и при большом объёме выборки, так и при малом объёме, прежде всего необходимо решить вопрос о принадлежности крайних вариант к генеральной совокупности. «Очистку» выборки осуществим путём исключения из выборки маловероятных вариант. При этом надо иметь ввиду, что если при большом объёме выборки относительный «вес» нескольких сомнительных вариант при вычислении усреднённых параметров сравнительно невелик, то при малом объёме выборки даже одно неправильное решение может заметно исказить результат усреднения.
Поэтому отбрасывание «ошибочных» вариант при малом объёме выборки является весьма ответственным этапом статистической обработки данных.
Исследование принадлежности всех элементов малой выборки к генеральной совокупности основано на использовании распределения Стьюдента (Госсет, статистик, англичанин). Требуется ответить на вопрос: является ли значимым или случайным наблюдённое значение t?
На этот вопрос даётся ответ таблицей значений критерия t при данном числе степеней свободы f и данной величине вероятности Р (см. приложение, таблица 3). Значение t определяется из формулы:
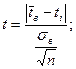
Здесь: 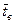 - среднее значение выборки;
- среднее значение выборки;
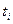 - исследуемое значение варианты;
- исследуемое значение варианты;
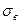 - исправленное среднее квадратичное отклонение выборки;
- исправленное среднее квадратичное отклонение выборки;
n – объём выборки.
При этом:
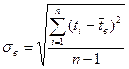 , где
, где 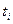 - варианты (i= 1; 2; …; n).
- варианты (i= 1; 2; …; n).
Число степеней свободы находится из соотношения:
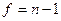 .
.
Суть критерия t состоит в следующем: если нормированное наблюдённое значение критерия t для испытуемой варианты 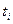 превосходит по абсолютной величине соответствующее табличное значение
превосходит по абсолютной величине соответствующее табличное значение 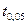 при Р =0,05, то t cчитается значимым; в прортивном случае t не является значимым и соответствующее
при Р =0,05, то t cчитается значимым; в прортивном случае t не является значимым и соответствующее 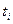 необходимо исключить из выборки. Исследование на принадлежность полученной из опыта крайней варианты
необходимо исключить из выборки. Исследование на принадлежность полученной из опыта крайней варианты 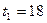 к генеральной совокупности приведено в таблице 10. При вычислении полагали
к генеральной совокупности приведено в таблице 10. При вычислении полагали 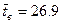 ; n = 7.
; n = 7.
Таблица 10.
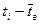 | 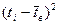 | 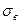 | Критерий t для 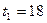 |
| 18 - 26,9 = - 8,9 | 79,21 | ||
| 2(24 – 26.9) = - 5,8 | 33,64 | ||
| 28 – 26,9 = 1,1 | 1,21 | ||
| 29 – 26,9 = 2.1 | 4,41 | ||
| 32 – 26,9 = 5.1 | 26,01 | ||
| 33 – 26.9 = 6.1 | 37,21 | ||
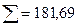 | 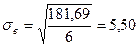 | 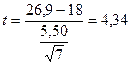 |
Из таблицы 3 приложения для f = 7 – 1 = 6 и Р = 0,05 находим значение 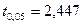 . Так как критерий
. Так как критерий 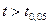 , то t – значимо и поэтому варианту
, то t – значимо и поэтому варианту 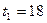 необходимо оставить в выборке.
необходимо оставить в выборке.
Аналогично предыдущему выполним расчёты для элемента 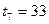 . Заметим, что если бы элемент
. Заметим, что если бы элемент 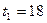 был бы исключён из выборки, то потребовалось бы заново рассчитать
был бы исключён из выборки, то потребовалось бы заново рассчитать 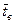 и
и 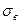 для объёма выборки n = 6.
для объёма выборки n = 6.
Так как 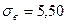 , а
, а 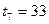 , то соответствующий наблюдённый критерий равен:
, то соответствующий наблюдённый критерий равен:
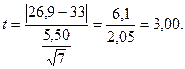
Как и в предыдущем случае, имеет место неравенство: 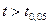 поэтому варианту
поэтому варианту 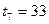 из выборки не исключаем.
из выборки не исключаем.
Анализ на систематический сдвиг выборочного среднего.
Согласно критерию А. А. Маркова, условием существования выборочного среднего является отсутствие систематического сдвига в погрешностях элементов выборки. Для анализа на систематический сдвиг выборочного среднего используем критерий Аббе, суть применения которого состоит в следующем:
1. Вычисляются несмещённые оценки 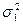 и
и 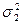 по формулам:
по формулам:
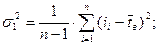
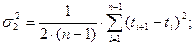
Здесь: 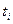 - варианты;
- варианты;
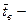 среднее значение «очищенной» выборки;
среднее значение «очищенной» выборки;
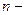 объём выборки.
объём выборки.
2. Определяется величина 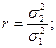
3. Найденное 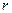 сравнивается с табличным
сравнивается с табличным 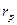 (см. приложение, таблица 4), которое находится по параметру
(см. приложение, таблица 4), которое находится по параметру 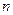 для заданного уровня значимости р = 0,05.
для заданного уровня значимости р = 0,05.
Если 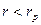 , то можно считать что оценки времени содержат систематический сдвиг выборочного среднего и их необходимо пересмотреть.
, то можно считать что оценки времени содержат систематический сдвиг выборочного среднего и их необходимо пересмотреть.
Из таблицы 10 выбираем 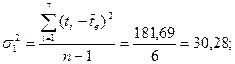
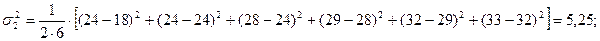
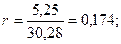
Найденное 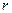 сравниваем с табличным: для
сравниваем с табличным: для 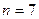 и
и 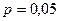 из таблицы 4 приложения определяем
из таблицы 4 приложения определяем 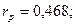 Так как
Так как 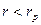 , то оценки времени содержат систематический сдвиг выборочного среднего и результаты эксперимента следует пересмотреть.
, то оценки времени содержат систематический сдвиг выборочного среднего и результаты эксперимента следует пересмотреть.
Доверительные границы для среднего значения в общей совокупности.
Определение точности средней выборочной с помощью распределения Стьюдента изложено в начале этой лекции, поэтому ограничимся только решением примера. Будем считать, что систематический сдвиг в оценке выборочного среднего отсутствует. Тогда из таблицы 3 приложения для 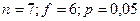 находим
находим 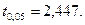 Далее, для
Далее, для 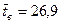 и
и 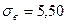 строим доверительные границы для выборочного среднего:
строим доверительные границы для выборочного среднего:
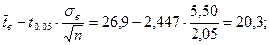
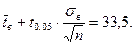
Итак, неизвестное среднее значение генеральной совокупности 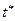 заключено в интервале:
заключено в интервале: 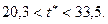
Пример для решения на практических занятиях.
Изучалась потребность размеров мужской обуви в г. Керчи в 1978 году. В результате многодневных опросов покупателей, проводимых в отделах «обуви» различных магазинов, получилась следующая сводная таблица:
Таблица 1.
| Размер | 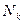 | 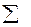 | |||||||||||
| Частота | 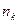 |
Найти основные параметры распределения полученной выборки.
Для получения точечных оценок числовых характеристик выборки и выдвижения гипотезы о наличии того или иного закона распределения гегнеральной совокупности составим рассчётную таблицу 2. При переходе к условным вариантам за «ложный» нуль С примем варианту С = 40. Шаг таблицы 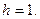 Тогда
Тогда 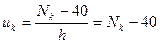 .
.
Таблица 2.
Варианта 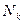 | Частота 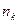 | Относит. частота 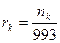 | Кумулят. распредел. 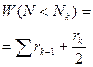 | Условная варианта 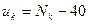 | 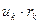 | 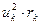 |
| 0,003 | 0,002 | -5 | -0,02 | 0,08 | ||
| 0,017 | 0,012 | -4 | -0,07 | 0,27 | ||
| 0,055 | 0,048 | -3 | -0,17 | 0,50 | ||
| 0,115 | 0,133 | -2 | -0,230 | 0,460 | ||
| 0,177 | 0,279 | -1 | -0,18 | 0,18 | ||
| 0,209 | 0,472 | |||||
| 0,190 | 0,671 | 0,19 | 0,19 | |||
| 0,127 | 0,830 | 0,25 | 0,51 | |||
| 0,067 | 0,928 | 0,204 | 0,60 | |||
| 0,033 | 0,978 | 0,13 | 0,53 | |||
| 0,007 | 0,997 | 0,04 | 0,18 | |||
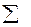 | 1,0 | 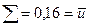 | 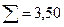 |
Точечную оценку среднего размера обуви получим по формуле:
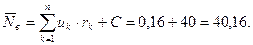
Оценка выборочной дисперсии составляет:
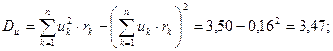 Тогда:
Тогда: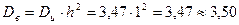 .
.
Стандарт (точечная оценка с. к. о.) равен: 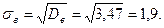
Сравним, далее, параметры выборки с аналогичными параметрами для нормального закона. Для этого воспользуемся первым и четвёртым столбцами таблицы 2 и построим график кумулятивного распределения (рис.1). Используя, далее, правило одного, двух и трёх «сигм», сравним полученные значения с цифрами, вытекающими из нормального закона распределения.
а). По правилу одного «сигма» имеем: 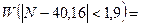 0.677. Для нормального закона распределения должно быть
0.677. Для нормального закона распределения должно быть 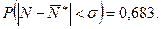
б). По правилу двух «сигм»: 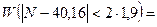 0,95. Должно быть 0,950.
0,95. Должно быть 0,950.
в). По правилу трёх «сигм»: 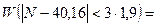 0,99. Должно быть 0,997.
0,99. Должно быть 0,997.
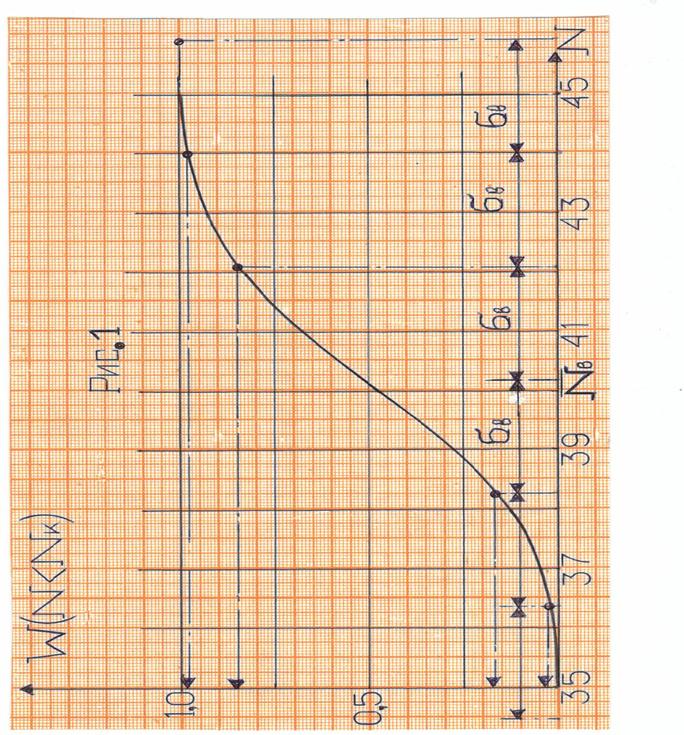
Близость полученнывх цифр к параметрам нормального распределения позволяет выдвинуть гипотезу о наличии нормального закона распределения в исследуемой выборке.
Определение принадлежности крайних вариант выборки
к генеральной совокупности.
Определение принадлежности крайних вариант к одной и той же гегнеральной совокупности удобно выполнять с помощью таблицы 3. При рассчёте принимали: 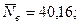
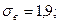 Вычисления производились по формуле:
Вычисления производились по формуле:
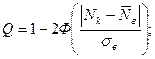
Таблица 3.
Крайняя варианта 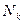 | 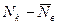 | 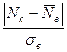 | 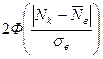 | Q | Заключение |
| -5,16 | 2,715 | 0,993 | 0,007 | Q < 0,05 | |
| -4,16 | 2,189 | 0,971 | 0,025 | Q < 0,05 | |
| -3,16 | 1,66 | 0,903 | 0,097 | Q > 0,05 | |
| 3,84 | 2,02 | 0,950 | 0,050 | Q = 0,05 | |
| 4,84 | 2,55 | 0,989 | 0,011 | Q < 0,05 |
Вывод: варианты 35, 36, 45 необходимо из выборки исключить как маловероятные (их вероятность менее 0,05).
Определение параметров «очищенной» выборки.
Для определения среднего размера и дисперсии «очищенной» выборки построим таблицу 4.
Таблица 4.
Варианта 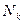 | Частота 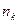 | Условная вар. 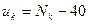 | 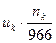 | 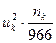 |
| -3 | -0,168 | 0,504 | ||
| -2 | -0,236 | 0,472 | ||
| -1 | -0,182 | 0,182 | ||
| 0.195 | 0,195 | |||
| 0,261 | 0,522 | |||
| 0,205 | 0,615 | |||
| 0,137 | 0,548 | |||
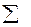 | 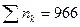 | 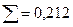 | 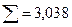 |
Точечная оценка среднего размера обуви равна:
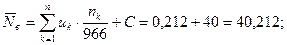
Оценка выборочной дисперсии составляет:
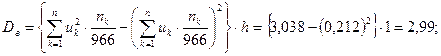 Оценка с. к. о. равна:
Оценка с. к. о. равна: 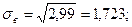
Построим, далее, графики наблюдённых и выравнивающих частот, для чего составим таблицу 5, используя полученные точечные оценки числовых параметров «очищенной» выборки.
Таблица 5.
Варианта 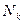 | Частота 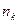 | 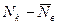  | 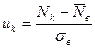 | 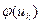 | 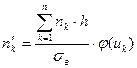 |
| -3,212 | -1,864 | 0,070 | 39,25 | ||
| -2,212 | -1,284 | 0,180 | 102,2 | ||
| -1,212 | -0,723 | 0,310 | 176,08 | ||
| -0,212 | -0,123 | 0.398 | 226,06 | ||
| 0,788 | 0,457 | 0.360 | 204,48 | ||
| 1,788 | 1,038 | 0,232 | 130,07 | ||
| 2,788 | 1,618 | 0,107 | 62,48 | ||
| 3,788 | 2,198 | 0,040 | 22,70 | ||
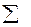 | 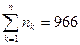 | 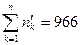 |
При вычислении выравнивающих (теоретических) частот в таблице 5 полагали:
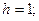
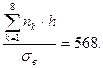
Графики наблюдённых и выравнивающих частот приведены на рис. 2. Точки, полученные из эксперимента, соединены отрезками прямых. Точки, полученные расчётным путём, соединены гладкой кривой.
Сравнивая графики, можно сделать вывод о том, что выравнивающие и наблюдённые частоты не значительно отличаются друг от друга, т. е. распределение оценок размеров обуви близко к теоретическому.
Но для того, чтобы уверенно сказать, что данные опроса покупателей свидетельствуют о нормальном расмпределении спроса на те или иные размеры обуви, необходимо применить более строгие количественные оценки, называемые критериями согласия.
Применим критерии Пирсона и Романовского для проверки выдвинутой статистической гипотезы о наличии нормального закона распределения. Для применения критерия Пирсона составим таблицу 6.
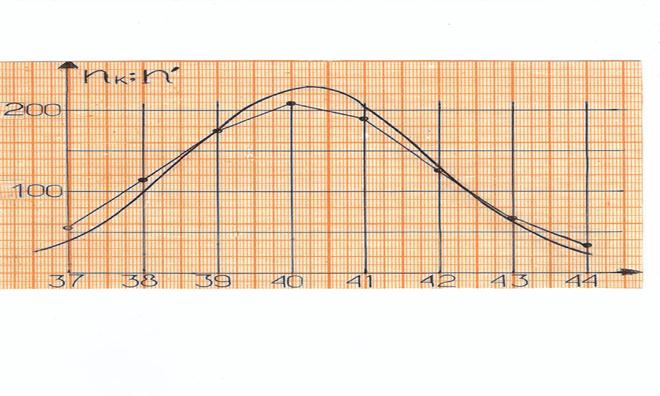
Рис. 2.
Таблица 6.
Наблюдённая частота 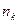 | Теоретическая частота 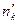 | 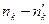 | 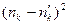 | 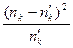 |
| 5,77 | ||||
| 1,41 | ||||
| -18 | 1,43 | |||
| -16 | 1,25 | |||
| -4 | 0,12 | |||
| 0,14 | ||||
| 4,35 | ||||
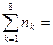 966 966 | 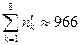 | 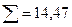 |
Число степеней свободы 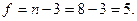 Здесь n – количество вариант. Для принятого уровня значимости 0,01 и 5 степеней свободы по таблице значений
Здесь n – количество вариант. Для принятого уровня значимости 0,01 и 5 степеней свободы по таблице значений 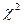 (см. таблицу 2 приложения) находим критическое значение критерия
(см. таблицу 2 приложения) находим критическое значение критерия 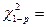 15,1. Так как
15,1. Так как 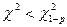 , то гипотезу о нормальном распределении генеральной совокупрости следует считать правильной.
, то гипотезу о нормальном распределении генеральной совокупрости следует считать правильной.
Проверка гипотезы при помощи критерия Романовского состоит в следующем:
если 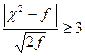 , то расхождение между эмпирическим и теоретическим распределениями можно считать существенным. Если же знак неравенства - противоположный, то расхождение можно считать случайным.
, то расхождение между эмпирическим и теоретическим распределениями можно считать существенным. Если же знак неравенства - противоположный, то расхождение можно считать случайным.
В нашем случае 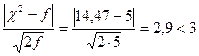 , т. е. расхождение – случайное.
, т. е. расхождение – случайное.
В заключение исследования вычислим доверительный интервал для оценки математического ожидания нормального распределения признака при известных точечных оценках среднего квадратического отклонения 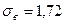 и выборочного среднего
и выборочного среднего 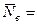 40,21. Объём вфыборки равен
40,21. Объём вфыборки равен 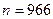 , зададимся доверительной вероятностью
, зададимся доверительной вероятностью 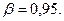
Для расчёта используем формулу:
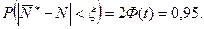 Здесь:
Здесь: 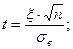
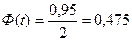 По таблице 1 приложения находим
По таблице 1 приложения находим 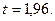
Из равенства 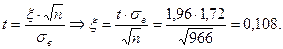
Искомый доверительный интервал равен:
40,21 – 0,108 < 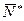 < 40,21 + 0,108; или: 40,102 <
< 40,21 + 0,108; или: 40,102 < 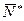 < 40,318.
< 40,318.
Пример использования результатов исследования при решении практических задач.
Предприниматель, имеющий обувной магазин, делает заказ на партию мужской обуви ходового фасона объёмом 500 пар. Для быстрой реализации партии и максимального удовлетворения спроса покупателей, заказанную обувь необходимо количественно разбить по размерам так, чтобы исключить невостребованные размеры. Для достижения этих целей можно использовать результат проведенного исследования. Для разбивки партии по размерам составляем рассчётную таблицу 7. Таблица 7.
Размер 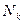 | 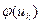 | 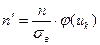 = = 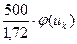 | Колич. пар 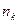 |
| 0,070 | 20,35 | ||
| 0,180 | 52,32 | ||
| 0,310 | 90,08 | ||
| 0,398 | 115,69 | ||
| 0,360 | 104,65 | ||
| 0,232 | 67,44 | ||
| 0,107 | 31,10 | ||
| 0,040 | 11,63 |
 2014-02-09
2014-02-09 10484
10484







