2014-02-09
750
И.
И.
Так как все слагаемые в суммах положительны, то:
Два сомножителя равны нулю, если равен нулю хотя бы один из сомножителей. Поэтому, если например: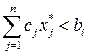 
, то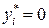 
,
если же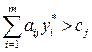 
, то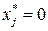 
, что и требовалось доказать.
Достаточность. Пусть для некоторых планов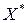 
и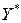 
пары двойственных задач выполняются соотношения:
если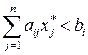 
, то 
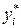= 0,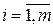 
;
или
если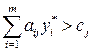 
, то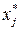 
= 0, j = 
,
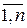Умножим неравенство (4.21) на 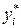, и суммируя по i, получим:
.
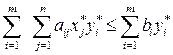Умножая неравенство (4.23) на 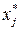, и суммируя по 
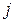, получаем:
.
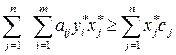Левые части в неравенствах равны, следовательно, равны и правые части:
,
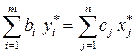Согласно достаточного признака оптимальности, планы 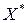и 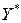являются оптимальными для прямой и двойственной моделей. Теорема доказана.
Вторая теорема двойственности с экономической точки зрения оценки оптимального плана – это мера дефицитности ресурсов. Ресурс, используемый в оптимальном плане производства полностью, является дефицитным, его оценка положительна. Дальнейшее его увеличение целесообразно. Если ресурс используется не полностью, то он избыточен, его дальнейшее увеличение не повлияет на эффективность предприятия. Двойственная оценка недефицитного ресурса равна нулю.
|
|
|
1. Система ограничений линейной оптимизационной модели, записанной в произвольной форме, содержит
1) только уравнения;
2) уравнения и неравенства;
3) только неравенства.
2. Система ограничений линейной оптимизационной модели, записанной в симметричной форме, содержит
1) только уравнения;
2) уравнения и неравенства;
3) только неравенства.
3. Система ограничений линейной оптимизационной модели, записанной в канонической форме, содержит
1) только уравнения;
2) уравнения и неравенства;
3) только неравенства.
4. Определить, в какой форме записана линейная оптимизационная модель:
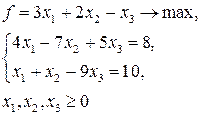
1) произвольной;
2) симметричной;
3) канонической.
5. Определить, в какой форме записана линейная оптимизационная модель:
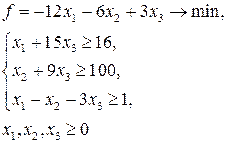
1) произвольной;
2) симметричной;
3) канонической.
6. Определить, в какой форме записана линейная оптимизационная модель:
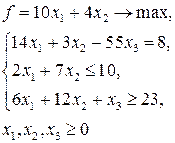
1) произвольной;
2) симметричной;
3) канонической.
7. Определить, в какой форме записана линейная оптимизационная модель:
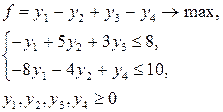
1) произвольной;
2) симметричной;
3) канонической.
8. Определить, в какой форме записана линейная оптимизационная модель:
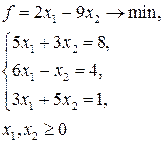
1) произвольной;
2) симметричной;
3) канонической.
9. Определить, в какой форме записана линейная оптимизационная модель:
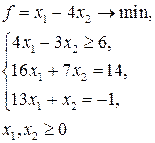
1) произвольной;
2) симметричной;
3) канонической.
10. При решении линейной оптимизационной модели графическим методом точкой максимума является
1) произвольная точка из области допустимых решений;
2) точка из области допустимых решений, последней оказавшаяся на линии уровня;
|
|
|
3) точка из области допустимых решений, первой оказавшаяся на линии уровня.
11. При решении линейной оптимизационной модели графическим методом точкой минимума является
1) произвольная точка из области допустимых решений;
2) точка из области допустимых решений, последней оказавшаяся на линии уровня;
3) точка из области допустимых решений, первой оказавшаяся на линии уровня.
12. При решении линейной оптимизационной модели графическим методом вектор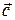 
1) параллелен линии уровня;
2) перпендикулярен линии уровня;
3) расположен произвольным образом относительно линии уровня.
13. Чтобы найти максимум целевой функции при решении линейной оптимизационной модели графическим методом, необходимо перемещать линию уровня
1) в направлении вектора ;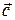
2) в направлении, противоположном вектору ;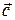
3) в любом направлении.
14. Чтобы найти минимум целевой функции при решении линейной оптимизационной модели графическим методом, необходимо перемещать линию уровня
1) в направлении вектора ;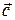
2) в направлении, противоположном вектору ;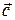
3) в любом направлении.
15. Разрешающая строка соответствует
1) наибольшему симплексному отношению;
2) наименьшему симплексному отношению;
3) произвольному симплексному отношению.
16. Разрешающий столбец соответствует
1) наименьшему положительному элементу в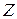 
-строке;
2) наибольшему положительному элементу в 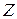-строке;
3) наименьшему отрицательному элементу в 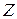-строке;
4) наибольшему отрицательному элементу в 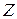-строке.
17. Разрешающий элемент в симплексной таблице
1) находится на пересечении разрешающего столбца и разрешающей строки;
2) находится на пересечении разрешающего столбца и f -строки;
3) выбирается произвольным образом.
18. Симплексные отношения – это
1) базисные координаты, деленные на элементы разрешающего столбца;
2) элементы разрешающей строки, деленные на элементы 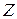-строки;
3) разность стоимости и суммы потенциалов для свободных клеток.
19. Решение линейной оптимизационной модели на максимум является оптимальным, если
1) в 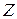-строке нет отрицательных элементов;
2) в 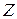-строке нет положительных элементов;
3) в столбце свободных членов нет нулевых элементов.
20. Если в 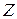-строке симплексной таблицы линейной оптимизационной модели есть хотя бы один нулевой элемент, то:
1) задача имеет множество оптимальных решений;
2) задача не имеет решений;
3) задача имеет единственное решение;
4) решение задачи не завершено.
21. Линейная оптимизационная модель называется вырожденной, если:
1) в столбце свободных членов симплексной таблицы есть хотя бы один нулевой элемент;
2) в столбце свободных членов симплексной таблицы все элементы положительные;
3) в симплексной таблице есть нулевые элементы.
22. Переменные исходной и двойственной моделей связаны следующим образом:
1) свободные переменные исходной модели соответствуют исходным переменным двойственной модели, базисные – базисным;
2) свободные переменные исходной модели соответствуют базисным переменным двойственной модели, базисные – исходным.
23. Каждая переменная двойственной модели соответствует
1) какой-либо переменной исходной задачи;
2) какому-либо ограничению исходной задачи.
24. Матрица коэффициентов двойственной модели – это
1) матрица коэффициентов исходной модели;
2) обратная к матрице коэффициентов исходной модели;
3) транспонированная матрица коэффициентов исходной модели.
25. Если какое-либо ограничение исходной модели является равенством, то соответствующая переменная двойственной модели
1) является отрицательной;
2) является неотрицательной;
3) не имеет ограничений.
26. Если какое-либо ограничение исходной модели является неравенством, то соответствующая переменная двойственной модели
|
|
|
1) является отрицательной;
2) является неотрицательной;
3) не имеет ограничений.
27. Если какая-либо переменная исходной модели является неотрицательной, то соответствующее ограничение двойственной модели является
1) равенством;
2) неравенством.
28. Если какая-либо переменная исходной модели не имеет ограничений, то соответствующее ограничение двойственной модели является
1) равенством;
2) неравенством.
29. Коэффициенты при переменных целевой функции двойственной модели – это
1) коэффициенты при переменных целевой функции исходной модели;
2) базисные координаты системы ограничений исходной модели;
3) свободные члены системы ограничений исходной модели.
30. Если ресурс в оптимальном плане производства используется полностью, то его оценка
1) положительна;
2) отрицательна;
3) равна нулю.
