X={xÎRn, x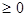 , Ax
, Ax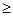 b}
b} b- вектор размерности n, A- матрица размерности m´n.
b- вектор размерности n, A- матрица размерности m´n.
f(x) = (c, x)- целевая функция (линейна)
ЗЛП: min f(x)-?, при xÎX- прямая задача линейного программирования.
Построим функцию Лагранжа.
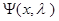 =(c, x)+(l1,b-Ax)+(l 2,-x), l1ÎRm, l2ÎRn (подгоняем под gi(x)£0).
=(c, x)+(l1,b-Ax)+(l 2,-x), l1ÎRm, l2ÎRn (подгоняем под gi(x)£0).
Тогда min(c, x) = max inf [(c, x)+(l1, b-Ax)+(l2, -x)], при l1³0, l2³0, xÎRn = (см. метод модификации функции Лагранжа) = max inf [(c- ATl1-l2, x)+(b, l1)]
при l1³0, l2³0, xÎRn =
(l1, Ax)=(ATl2, x)
= max 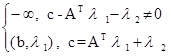 , при l1³0, l2³0
, при l1³0, l2³0
= max (b, l1) (при l1³0, l2³0, с=ATl1+l2) = max (b, l1) (при l1³0, с ³ATl1)
= max (b, l) = (c, x*), с ³ATl, l ³0
max (b, l), с ³ATl, l ³0- двойственная ЗЛП.
Таким образом, решение исходной ЗЛП может быть сведено к решению новой ЗЛП: максимизация (b, l) по множеству, определенному условиями с ³ATl,
l ³0.
Утверждения:
1. Вектор состояния l двойственной ЗЛП имеет размерность m- количество ограничений в исходной задаче (размерность вектора Ax).
2. Количество ограничений (кроме l ³0, неотрицательных) совпадает с размерностью вектора состояний в исходной задаче (вектора x).
3. Суммарное количество ограничений совпадает с (n + m) в обеих задачах.
|
|
|
4. Двойственная задача к двойственной дает исходную.
Когда какую задачу решать - зависит от числа ограничений и от размерности x.
Утверждение:
Двойственные переменные можно рассматривать как коэффициент чувствительности целевой функции к изменению параметров задачи.
Пусть x*, l *- решения прямой и двойственной задач, причем эти решения единственны (достиг. в одной точке минимум x и в одной максимум l)
Тогда f(x*) = (b, l*), несколько изменим b: b®b+Db Þ min увеличился на
(Db, l*). При сдвиге b градиенты не изменились, li остались теми же.
Обозначим h(b) = min f(x), Ax ³b, x ³0.
Тогда при малых Db:
h(b+Db) = h(b) + (Db, l*), следовательно при Db® 0 получим:
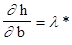 , для компонент векторов
, для компонент векторов 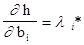
 2014-02-09
2014-02-09 403
403








