Теорема.
Число 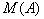 всех подмножеств множества A из n элементов равно
всех подмножеств множества A из n элементов равно 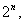
Следствие. Справедливо равенство
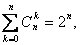
поскольку 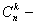 число k - элементных подмножеств множества из n элементов, то сумма в левой части есть число всех подмножеств.
число k - элементных подмножеств множества из n элементов, то сумма в левой части есть число всех подмножеств.



а) Объединение конечного числа счетных множеств счетно
б) Объединение счетного числа счетных множеств счетно
в) Объединение конечного числа конечных множеств конечно или счетно

Теорема. Пусть А и В счетные множества. Тогда декартово произведение 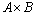 также является счетным множеством.
также является счетным множеством.
Доказательство. Перечислим элементы множеств А и В: А = 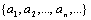 ,
, 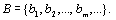 Тогда
Тогда 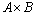 =
= 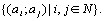 Разобьем
Разобьем 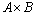 на счетное объединение счетных множеств:
на счетное объединение счетных множеств:
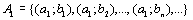 ,
,
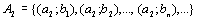 ,
,
.…………………………………….
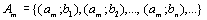 .
.
Очевидно, что 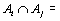 Ø при
Ø при 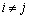 , т.к.
, т.к. 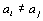 , и
, и 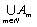 = А
= А  В, то есть
В, то есть 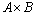 есть объединение счетного числа счетных попарно непересекающихся множеств. Значит
есть объединение счетного числа счетных попарно непересекающихся множеств. Значит 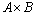 счетно.
счетно.
Следствие. Пусть 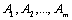 – счетные множества, тогда
– счетные множества, тогда 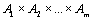 – счетно.
– счетно.
Теорема. Отрезок 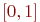 равномощен множеству всех бесконечных последовательностей нулей и единиц.
равномощен множеству всех бесконечных последовательностей нулей и единиц.
Доказательство. В самом деле, каждое число  записывается в виде бесконечной двоичной дроби. Первый знак этой дроби равен
записывается в виде бесконечной двоичной дроби. Первый знак этой дроби равен  или
или 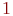 в зависимости от того, попадает ли число
в зависимости от того, попадает ли число 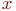 в левую или правую половину отрезка. Чтобы определить следующий знак, надо выбранную половину поделить снова пополам и посмотреть, куда попадет
в левую или правую половину отрезка. Чтобы определить следующий знак, надо выбранную половину поделить снова пополам и посмотреть, куда попадет 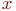 , и т.д.
, и т.д.
Это же соответствие можно описать в другую сторону: последовательности 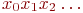 соответствует число, являющееся суммой ряда
соответствует число, являющееся суммой ряда
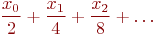
Описанное соответствие пока что не совсем взаимно однозначно: двоично-рациональные числа (дроби вида 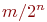 ) имеют два представления. Например, число
) имеют два представления. Например, число 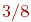 можно записать как в виде
можно записать как в виде 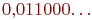 , так и в виде
, так и в виде 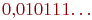 Соответствие станет взаимно однозначным, если отбросить дроби с единицей в периоде (кроме дроби
Соответствие станет взаимно однозначным, если отбросить дроби с единицей в периоде (кроме дроби 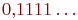 , которую надо оставить). Но таких дробей счетное число, поэтому на мощность это не повлияет.
, которую надо оставить). Но таких дробей счетное число, поэтому на мощность это не повлияет.
Теорема. Квадрат (со внутренностью) равномощен отрезку.
Доказательство. Квадрат равномощен множеству 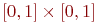 пар действительных чисел, каждое из которых лежит на отрезке
пар действительных чисел, каждое из которых лежит на отрезке 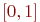 (метод координат). Мы уже знаем, что вместо чисел на отрезке можно говорить о последовательностях нулей и единиц. Осталось заметить, что паре последовательностей нулей и единиц
(метод координат). Мы уже знаем, что вместо чисел на отрезке можно говорить о последовательностях нулей и единиц. Осталось заметить, что паре последовательностей нулей и единиц 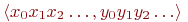 можно поставить в соответствие последовательность-смесь
можно поставить в соответствие последовательность-смесь 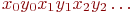 и что это соответствие будет взаимно однозначным.
и что это соответствие будет взаимно однозначным.
Теорема. Если множество  бесконечно, а множество
бесконечно, а множество  конечно или счетно, то объединение
конечно или счетно, то объединение  равномощно
равномощно  .
.
 2014-02-09
2014-02-09 6484
6484