2014-02-09
1087
Мощности конечных множеств - натуральные числа, и их можно складывать, умножать, возводить в степень. Эти операции можно обобщить и на мощности бесконечных множеств, и делается это так.
Пусть 
и 
- два множества. Чтобы сложить их мощности, надо взять мощность множества 
, если и не пересекаются. Если они пересекаются, то их надо заменить на непересекающиеся равномощные им множества 
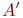и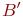 
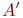. Мощность объединения и будет суммой мощностей множеств и . Множества и 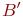можно выбрать следующим образом: положим 
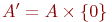и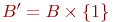 
.
Произведение мощностей – мощность декартова произведения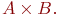 
Возведение в степень. Рассмотрим (для данных и ) множество всех функций вида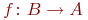 
(их область определения есть , а область значений содержится в ). Это множество обозначается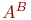 
, и его мощность и будет результатом операции возведения в степень.
Если множества и конечны и содержат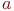 
и 
элементов соответственно, то 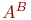содержит как раз 
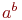элементов. В самом деле, определяя функцию 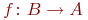, мы должны определить ее значение на каждом из элементов. Это можно сделать 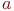способами, так что получаем всего 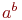вариантов.
|
|
|
Пример.
Обозначим через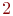 
множество из двух элементов, например, 
. 
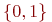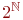по определению это множество функций 
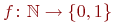. Такие функции - это последовательности нулей и единиц, только вместо 
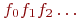пишем
Свойства сложения и умножения (коммутативность, ассоциативность и дистрибутивность) сохраняют силу и для арифметики мощностей:
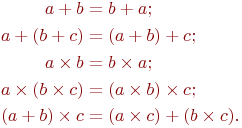
Формально их следует читать, избегая слова " мощность" как самостоятельного объекта: например,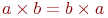 
означает, что 
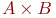и 
равномощны (и это легко проверить: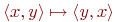 
будет взаимно однозначным соответствием между ними).
Свойства, включающие возведение в степень:
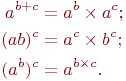
Проверим первое из них. Элементами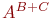 
(и 
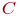не пересекаются) являются функции со значениями в , определенные на 
. Такая функция состоит из двух частей: своего сужения на (значения на аргументах из остаются теми же, остальные отбрасываются) и своего сужения на 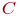. Тем самым для каждого элемента множества 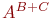получаем пару элементов из 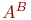и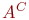 
. Это и будет искомое взаимно однозначное соответствие.
Мощность счетного множества символически обозначается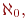 
мощность континуума (отрезка или множества бесконечных последовательностей нулей и единиц) обозначается 
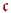. По определению, 
.
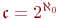(Обычно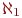 
обозначает наименьшую несчетную мощность. Гипотеза континуума утверждает, что 
.)
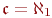Известные свойства счетных множеств можно записать следующим образом:
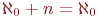для конечного 
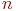(объединение счетного и конечного множеств счетно);
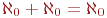(объединение двух счетных множеств счетно);
(объединение счетного числа счетных множеств счетно).
Отсюда можно формально получить многие факты манипуляциями с мощностями.
|
|
|
Пример
1) цепочка равенств
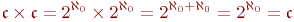
показывает, что прямая и плоскость равномощны.
Аналогично,
2) 
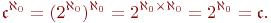
3) 
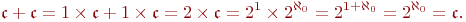
4) 
.
5) Приведенные свойства мощностей полезно сочетать с теоремой Кантора- Бернштейна. Например
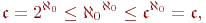
поэтому 
(множество всех бесконечных последовательностей натуральных чисел имеет мощность континуума).
