Счётные множества

Множество, равномощное множеству всех натуральных чисел, называется счётным.

Мощность множества натуральных чисел обозначается א₀ = |N|.

Не более чем счётное множество – множество счётное или конечное.

Этим определением мы достали из класса эквивалентности, который назвали счётным, одного представителя – множество натуральных чисел – и теперь есть с чем сравнивать другие множества.

Любая биекция ν: N → M называется нумерацией множества М. М={a_i| i= 0, 1,2, …}.

Таким образом, если найдена нумерация некоторого множества, то тем самым доказано, что оно счётное. Элементы счётного множества называют также последовательностью.

.

Пусть задан алфавит А – некоторое множество символов, называемых также буквами. Назовём словом в данном алфавите конечный ряд букв, написанных друг за другом. Иногда удобно рассматривать пустое слово, совсем не содержащее букв – его обозначают Λ.

Докажем, что в любом языке имеется счётное множество слов

Теорема. Если алфавит А конечен, то множество слов в алфавите А* счётно.

□. Пусть А={S₁, S₂, …, S_p-1}, p>1. Определим биекцию ν: N → А* следующим образом: ν(0)= Λ; произвольное число n сначала запишем в р -ичной системе счисления: n=a_kp^k+a_k-1p^k-1+…+a₀, 0≤a_i ≤ p-1 т.е. n=[a_k…a₀]_p а затем положим ν(n)=Sa_n….Sa₀. Слово, определяемое р -ичным числом, единственное. И наоборот, каждому слову соответствует единственное число – следовательно, это биекция. ■

Следствие: слов в алфавите {0,1,2,…,9} – счётное число. Это – проверка на корректность – мы снова подтвердили счётность множества натуральных чисел.

Теорема. Любое подмножество счётного множества не более чем счётно.

□ Пусть А – счетно. Значит, его элементы могут быть перенумерованы: {а₁, а₂, …, a_n,…}. Элементы любого подмножества ВÍА можно расположить в порядке возрастания номеров: 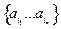. Следовательно, подмножество имеет нумерацию ν(n)= ■

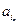Теорема. Любое бесконечное множество содержит счётное подмножество.

□ Пусть А₀ - бесконечное множество. Значит, оно непусто и $ а₁ ÎА₀. Положим А₁=А ₀\{a₁}. А₁ не пусто, т.к. в противном случае А₀ ={a₁}, что противоречит предположению о бесконечности А₀. Продолжим процедуру: в А₁ найдётся a₂, положим А₂=А₁\{a₂}=А₀\{a₁, a₂} …и т.д.

На n-шаге получим: А_n=А₀\{a₁, …,a_n} непусто, т.к. в противном случае А₀={a₁, …,a_n}. Кроме того, по построению a_i≠a_k, если i ≠ k – элементы попарно различны. Тогда $ а_n ÎА_n и, по построению, А_n+1= А_n\{a_n} непустое множество.

Таким образом, по индукции мы построили множество, состоящее из попарно различных элементов {а₁, а₂, …, a_n,…}Î А₀ с нумерацией ν(n)=a_n. ■

Из доказанных теорем следует, что счётное множество является самым минимальным по мощности из всех бесконечных множеств – потому, наверно, его и называют алеф ноль.

Теорема. В любом бесконечном множестве можно выделить два непересекающихся между собой счётных множества. Доказательство – разбиение на чётную и нечётную нумерации.

Семейство множеств {A_i}|_iÎI называют не более чем счётным, если таково множество I.

Теорема. Объединение любого не более чем счетного семейства множеств счётно.

Занумеруем элементы объединения семейств следующим образом:

a) I конечно; б) I счетно

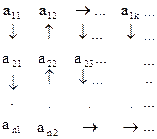
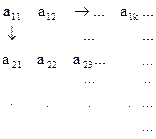
Последовательность (a₁₁,a₂₁,a₁₂,a₂₂,a₃₁,…) – нумерация. Принцип её построения таков – сначала фиксируется N = 2 и записываются а_ik такие, что i+k = N. Затем N → N+1 и все повторяется.

Замечание: В семействах могут быть одинаковые элементы

Следствие. Множество А* всех слов в счётном алфавите А счётно. Пусть задана нумерация в А: A={а₁, а₂, …, a_n,…}

Обозначим через А_n конечный алфавит: А_n={а₁, а₂, …, a_n}. Любое слово в А* состоит из конечного числа букв (по определению), поэтому оно является словом в некотором конечном алфавите, а именно в A_k, k=max(k₁, k₂, …, k_n). Т.о., множество всех слов в алфавите А есть объединение счётного числа множеств А₁, А₂,…, А_n.

Пример. Алгебраические числа. Корни произвольного многочлена a_nxⁿ+… + a₀, где а_k – целые числа, называются алгебраическими числами. Многочлен можно рассматривать как слово в конечном алфавите: А={0,1,2,…,*,+,-} – множество таких слов счетно, а корней у многочлена конечное число. Поэтому и множество всех алгебраических чисел счётно.

Теорема. Множество значений функции, определённой на счётном множестве, не более чем счётно. ν(n) = f(a_n) – нумерация.

Теорема. Пусть А – бесконечное множество, а B – его не более чем счётное подмножество. Тогда, если множество A\B бесконечно, то оно равномощно множеству A.

Выберем из A\B счётное подмножество C; по построению B∩C =О. Объединение B и C счётно, поэтому существует биекция f: BÇC→C. Надо построить биекцию А→ A\B. Построим:

(А\ (B Ç C)) Ç (B Ç C)= А→ A\B=(А\ (BÇC))ÇC

Следствие: если A бесконечно, а B не более чем счётно, то объединение AÇB не более чем счетно.