Перевозок.
Блокирование перевозки или запрещение
Транспортных издержек.
Предположим что имеется m-производителей и n-покупателей.
Ai = (i = 1,m) Bj = (j = 1.n)
Известны производственные затраты di (i = 1,n)
Спланировать перевозки так чтобы суммарные (производственные и транспортные) затраты были минимальными.
Нужно решить обычную транспортную задачу, затраты которой Cij = Cij + d
Очень часто на практике при решение Т.З либо какой-то производитель или потребитель закладывает “запрет“на продукцию.
Если это производитель – то он может запретить перевозку своего товара любому потребителю своей продукции.
Если это потребитель – то он может запретить перевозку товара к себе любому производителю с которым нехочет иметь дело.
В этом случае клетка с номером i, j должна быть заблокирована. И осуществляется это следующим образом. В клетку с номером i, j место Cij записываем число m (очень большое положительное число).
Пусть имеются m исполнителей которые должны быть назначены на выполнение n работ.
|
|
|
Известна матрица C. С – затраты при назначении i – исполнителя на выполнение j – вида работ C = Cij
Произвести назначение таким образом, чтобы каждый исполнитель выполнял только 1 работу, и каждая работа выполнялась только 1 исполнителем. При этом затраты должны быть минимальными.
Возможные постановки:
Ai – Экономисты. (i = 1,m) Bj – Работа. (j = 1,n) Cij – Затраты.
Ai – Строительные механизмы. Bj –Площади. Cij – производительность.
Математическая модель.
Предположим m=n. Введем целочисленное обозначение пусть Xij 1- i-ый на j—ю, 0 в противном случае. Получим матрицу из элементов 0 и 1. Так как исполнитель может быть назначен на одну работу и одна работа может быть выполнена только одним исполнителем в каждой строке и столбце только одна 1. Система ограничение все = 1 (по строкам и столбцам) Х –(0;1) Z=двойная сумма СijXij ->min =>Задача о назначениях является частной Т.З., где ai и bj=1 причем r=m+n-1=2n-1>n –решение всегда выраждена.
Теоремы на которых основаны решения задачи о Назначениях.
Т. Кенинга Если элементы матрицы С, разделить на два класса, на основании свойства R, то минимальное число линий содержащих все элементы со свойством R = максимальному числу таких элементов со свойством R, не какие два из которых не лежат на одной прямой.
Теорема: Решения задачи о назначениях не изменится если к матрице прибавить или отнять из каждого столбца иил каждой строки одно и тоже число.
С=¦Сij¦
C1=¦Cij-Ui+Vj¦ - док-ть что Х не изменится.
Z1(X)=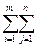 (Cij-Ui+Vj)Xij=
(Cij-Ui+Vj)Xij=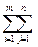 CijXij-
CijXij-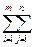 UiXij+
UiXij+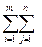 VjXij=Z(x)-
VjXij=Z(x)- 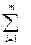 Ui
Ui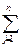 Xij +
Xij +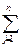 Vj
Vj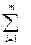 Xij = > Z1(x)=Z(x)-
Xij = > Z1(x)=Z(x)- 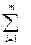 Ui+
Ui+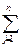 Vj – очевидно что решение не изменилось
Vj – очевидно что решение не изменилось 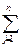 Xij=1
Xij=1
Изменилось только значение функции
3) Если можно найти такую матрицу назначений функции Х, для которой значение функции Z будет равно=0 то Х является оптимальным решением данной задачи. Если Xij>=0; Сij>=0, то произведение их Сij*Xij>=0 сумма их тоже >=0. Очевидно что самое минимальное число 0, Х – будет являться решением задачи. => назначение производится по 0.
|
|
|
Алгоритм решения.
1. Все действия выполняются с матрицей С
2. Из каждой строки матрицы вычитается минимальный элемент этой строки
3. Так же и столбец
4. Минимальным числом линий вычеркиваем все 0, если число линий = n то произодим назначение.
5. Если число линий меньше n, то выбираем минимальный элемент из не вычеркнутых и вычитаем его из не вычеркнутых, а перечеркнутым дважды прибавляем.
Задача коммивояжера.
Постановка задачи:
Известно что комиваяжер выезжает из города и должен посетить A1, A2, A3,…, AK городов и вернутся в город A1. Известно расстояние Cij между городами Ai – Bj причем известно Cij ¹ Cji.
Cij = Cjj = ¥. Спланировать маршрут таким образом, чтобы расстояние L для этого маршрута (I1, I2 , I3,…, Ik) было кротчайшим.
Математическая модель этой задачи:
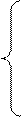
х11+х12+…+х1k =1
x21+x22+…+x2k =1
xk1+xk2+…+xkk = 1
x11+ +x21 +xk1 = 1
x12+ x22+ xk2 = 1
x1k+ x2k+ +xkk = 1
Z = 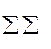 CijXij ® min
CijXij ® min
Маршрут – это цикл.
Метод ветвей и границ.
1. Допустимые множества в задачи коммивояжера
F(x) ® min (1,2,3,…,K,1)
XÎД (1,3,2,…,K,1)
Для задачи допустимым планом является маршрут от 1 города, 2, 3. О.Д.Р. – есть множество маршрутов (перестановки).
2. Нижняя оценка (граница).

 |
Д
Нижней оценкой к x где Д* множество – называется такое число x* = d(Д*) удовлетворяет условию x* £ f(x) где XÎД*.
 2014-02-09
2014-02-09 523
523







