Метод Гаусса — Зайделя

Метод Гаусса—Зайделя предусматривает поочередное нахождение частных экстремумов целевой функции по^: каждому фактору х_i (i=l, 2,..., п). При этом на каждом i-м этапе стабилизируют n—1 факторов и варьируют только один, i-й фактор. Графическая интерпретация метода дана на рис..6.2, где на плоскости двух факторов изображена функция отклика у топографическим способом с помощью замкнутых линий постоянного уровня этой оптимизируемой выходной функции. Эти линии на рис. 6.2 соответствуют некоторым относительным величинам, однако, как указывалось выше, форма функции отклика до начала исследования обычно неизвестна. Путь движения обозначен точками М. Задачу поиска максимума методом Гаусса—Зайделя решают в несколько этапов, объединенных в циклы.

* Под помехоустойчивостью метода будем понимать его способность правильно оценивать направление рабочего движения, а также способность быстро и точно приводить рабочую точку в область экстремума, несмотря на наличие помех e.

Рассмотрим процедуру метода с иллюстрацией двухфакторного примера.

I этап. 1. Выбирают основную (начальную, базовую) точку (на рис. 6.2 это точка Мо), обычно она соответствует номинальному режиму ведения технологического процесса 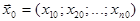. Иногда эту точку выбирают в центре области, которую желательно исследовать, либо в центре области ограничений *, если они имеются.:

2. Выбирают интервал (ступень) варьирования Dх₁ (рис. 6,2) по фактору х₁. Очевидно, что ступень варьирования не должна быть слишком малой, иначе движение к экстремуму окажется замедленным. Кроме того, на интервале варьирования Dх_i (i =1,2,..., п) изменение целевой функции Dу должно быть существенно большим, чем погрешность ее измерения d_у (не менее чем в 5—10 раз).

3. Определяют координаты пробных точек М₁ и М₂:

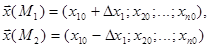(6.5)

4. В точках М₁ и М₂ ставят пробные опыты (для повышения точности результатов могут выполняться параллельные опыты), измеряют отклики у(М₁) и у(М₂).

5. Сравнивают полученные отклики, и если

у(М₂)>y(M₁) (6.6)

(как на рис. 6.2), то совершают.рабочее движение, на один рабочий шаг Dх₁ по направлению 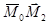в точку М₃.

6. Аналогичные шаги продолжают в том же направлении до тех пор, пока на каком-то k-м шаге не окажется, что

у(М_k)<y(M_k-1) (6.7)

т. е, значение отклика в очередной, k- й рабочей точке станет уменьшаться, — это и служит признаком достижения частного экстремума. За частный экстремум принимают (k— 1)-ю точку с откликом у(М_k-1). На рис. 6.2 это точка М₆.

II этап. Его проводят в том же порядке, что и I этап, с той. лишь разницей, что стабилизируют все факторы, кроме х₂. За новую базовую точку принимают точку с координатами **

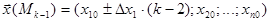, (6.8)

а х₂ варьируют на выбранную по аналогичным условиям величину интервала варьирования Dх₂. По достижении частного кстремума по фактору х₂ точку нового частного экстремума принимают за новую базовую точку. На рис. 6.2 это точка М₁₁.

* При таком выборе базовой точки все направления оказываются равноправными, а это важно в случае, когда заведомо ничего неизвестно о том, где, хотя бы примерно, расположен экстремум.

** Если начало движения, из точки М₀ сразу совпало с возрастанием у, то в равенстве (6.8) вместо k—2 берут k—1.

Первый цикл продвижения к экстремуму заканчивается n-м этаном, на котором стабилизируют все факторы, кроме x_n. Для него выбирают ступень варьирования Dх_n и совершают пробное, а затем рабочее движение до достижения частного экстремума по фактору x_n. Если экстремум не достигнут, то выполняют второй цикл поиска.

Второй цикл, как и первый, начинается с I этапа, на котором варьируют фактор х₁ при стабилизации остальных х_i (i¹1), затем последовательно выполняют п этапов по каждому из п факторов.

Поисковое шаговое достижение к экстремуму заканчивают по достижении такой точкой факторного пространства, при движении из которой в любую сторону по всем п факторным осям x_i в положительном или отрицательном направлениях значения отклика оказываются меньшими. Такую точку принимают за экстремум (максимум).

Достоинства метода Гаусса—Зайделя: 1) очевидная простота стратегии и наглядность; 2) высокая помехозащищенность в смысле выбора направления движения.

Недостатки: 1) путь к главному экстремуму оказывается обычно долгим, особенно при большом числе n факторов; 2) в условиях крупного промышленного производства оказывается трудным застабилизировать п— 1 фактор на длительное время; 3) если поверхность отклика имеет сложную форму (узкие гребни, овраги и т. п.), то использование метода может привести к ложному ответу на вопрос о месте расположения экстремума; 4) метод не дает информации о взаимодействиях факторов.

Исторически метод Гаусса — Зайделя известен как первый из рассматриваемых. В настоящее время он иногда применяется при машинном эксперименте.

6.3. Градиентные методы

Градиентные методы имеют несколько разновидностей, различающихся правилами выбора ступеней варьирования и рабочих шагов на каждом этапе движения к экстремуму. Сущность стратегии всех этих разновидностей состоит в том, что на каждом этапе вокруг очередной базовой точки организуют пробные эксперименты, по результатам которых оценивают новое направление градиента, после чего в этом направлении совершают один рабочий шаг. Напомним, что вектор-градиент в n-факторном пространстве определяется соотношением

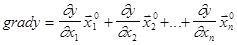, (6.9)

где 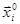(i = I, 2,..., п) —единичные направляющие векторы (орты), расположенные вдоль факторных осей; 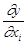частная производная целевой функции по i -му фактору. Пробные опыты (по два в точках, расположенных на прямых, параллельных каждой факторной оси и проходящих через базовую. точку) проводят с целью получить приближенные оценки частных производных. Рассмотрим две разновидности градиентных методов.

Метод градиента (обычный) осуществляется по следующей процедуре.

1. Выбирают начальную (базовую) точку по правилам, изложенным в п. 6.2. На рис. 6.3 это точка L₀

2. Выбирают интервал варьирования Dx_i по каждому из факторов x_i(i=l,2;;.., п), пользуясь уже известными правилами.

3. Определяют координаты пробных точек (рис..6,3), Например, вдоль направления, параллельного факторной оси x₁ ими являются точки L₁, L₂ с координатами

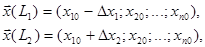(6.10)

т, е. варьируют один фактор х₁ при стабилизации остальных факторов на базовом уровне. Аналогично вычисляют координаты пробных точек вдоль направлений, параллельных: остальным факторным осям х₂, х₃,..., х_n. В пробных точках, ставят опыты и получают значения целевой функции у.

4. По результатам пробных опытов вычисляют оценки составляющих вектор-градиента в точке L₀ для каждого i-ro фактора:

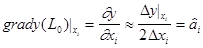. (6.11)

В частности, для фактора х₁ по результатам опытов в точках L₁ и L₂ вычисление выполняют по формуле

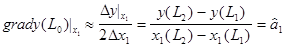. (6.12)

Как известно, частные производные являются коэффициентами а_i (i=1, 2,..., п; i¹0) уравнения плоскости, касательной к поверхности отклика в точке L₀:

y= a₀+a₁x₁+a₂x₂+...+a_nx_n. (6.13)

Оценки 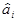коэффициентов получают по формуле (6.11).

5. Находят координаты рабочей точки на направлении градиента. Для этого выбирают параметр рабочего шага r_гр и вычисляют координаты первой рабочей точки по всем факторным осям х_i(i=1, 2,..., п):

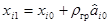. (6.14)

На рис. 6.3 первой рабочей точкой является точка L₅. Чтобы из основной точки L₀ попасть в точку L₅, от L₀ откладывают в масштабе отрезки, равные 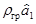и 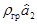, причем если 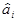<0, то по соответствующему фактору отрезок откладывают в отрицательном направлении от точки L₀, т. е. для фактора x₁ — влево от точки L₀, а для фактора x₂—вниз от точки L₀. Если 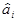> О, то отрезки 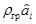откладывают в положительном направлении от основной точки.

6. Первую рабочую точку принимают, за новую базовую точку и вокруг нее организуют новые пробные опыты для оценивания нового направления градиента, после чего совершают новый рабочий шаг (на рис. 6.3—в точку L₁₀). В общем случае в каждой k- й рабочей точке по результатам пробных опытов вокруг н ес получают оценки составляющих градиента 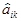и совершают (k+1)-й рабочий шаг (k=0, 1, 2,...) в точку с координатами

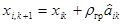. (6.15)

7. Рабочее движение производят до тех пор, пока на очередном шаге все составляющие градиента не станут пренебрежимо малыми, т. е. все 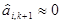(i= 1, 2,..., п). Для этого достаточно, чтобы выполнялось неравенство*

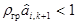. (6.16)

Если по результатам пробных опытов в (k+1)-й рабочей точке выполняется условие (6.16), то движение к экстремуму прекращают и эту рабочую точку принимают за точку экстремума.

Достоинства метода градиента: 1) достаточная простота стратегии; 2) повышенная по сравнению с методом Гаусса — Зайделя скорость движения к экстремуму (эффективность).

Недостатки: 1) большая чуткость к помехам ев отношении выбора направления, рабочего движения; 2) в случаях, когда поверхность отклика имеет сложную форму, метод градиента может не привести к истинному экстремуму; 3) если поверхность отклика достаточно пологая, то в условиях помех метод мало эффективен в смысле точности выхода к экстремуму; 4) как и метод Гаусса — Зайделя, метод градиента не дает информации о взаимодействиях факторов (взаимодействия характеризуют степень кривизны поверхности отклика).

* Так как на СМОУ-1 МЭИ факторы x_i могут принимать только целочисленные значения, то при выполнении работы следует пользоваться именно этим неравенством.

Метод Кифера—Вольфовица отличается; от описанного выше обычного метода градиента тем, что если в первом из них размеры интервалов варьирования Dx_i при постановке пробных опытов и параметр r_гр рабочего шага остаются неизменными на любом рабочем шаге, то в рассматриваемом методе Dx_ikи r_грk выбирают в зависимости от номера k рабочего шага:

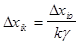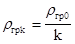, , (6.17)

где Dx_io — начальный интервал варьирования в основной точке L_o; r_гр0 — начальное значение параметра рабочего шага; k— номер рабочего шага (k =1, 2,...); g — постоянная степень, обычно выбираемая в пределах 0<g<0,5. Чаще всего полагают g=0,25.

Если в методе градиента фактический размер k- го рабочего шага уменьшается только из-за уменьшения градиента, т. е. крутизны наклона поверхности отклика, при приближении к области экстремума, то в методе Кифера —Вольфовица фактический размер рабочего шага уменьшается, как мы видели, и в прямой зависимости от номера этого шага.

Достоинством метода Кифера — Вольфовица по сравнению с немодифицированным методом является его повышенная точность отыскания экстремальной точки, если поверхность отклика достаточно крутая, а экстремум находится от базовой точки не слишком далеко. Недостатком этого метода является его низкая эффективность в условиях пологих поверхностей отклика. При очень пологих поверхностях отклика метод Кифера - Вольфовица вообще не приводит к цели: рабочие шаги становятся сравнимыми с погрешностями измерения до достижения экстремума. Остальные достоинства и недостатки, а также вся процедура работы такие же, как и в методе градиента.*

6.4. Метод крутого восхождения (метод Бокса—Уилсона)

Метод крутого восхождения предложен Дж. Боксом и К. Уилсоном как синтез лучших черт градиентных методов и метода Гаусса—Зайделя, причем пробные опыты для выяснения направления движения также выполняют по-особому — методом ПФЭ (или ДФЭ). От градиентных методов здесь воспринято выполнение рабочего движения вдоль вектор-градиента, определенного в районе исходной (базовой) точки, а от метода Гаусса — Зайделя взят, принцип продвижения не на один рабочий шаг (как в методе градиента), а до достижения частного экстремума функции отклика на направлении градиента, без его корректировки на каждом рабочем шаге. Проведение пробных опытов методом ПФЭ (или ДФЭ) позволяет более точно оценивать направление градиента, чем при традиционном методе градиента. Действительно, из сравнения рис. 6.4 и рис. 6.3 и исходя из расчетной формулы (6.1,1) для оценок и, коэффициентов в методе градиента и в методе крутого восхождения'(см. тему 3) можно заключить, что при числе факторов п = 2 количество точек для пробных опытов в обоих методах равно 4, т. е. одинаково. Но если каждую оценку 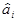в методе градиента получают по результатам опытов лишь в двух пробных точках (при любом числе n факторов), то в методе крутого восхождения—по результатам опытов во всех четырех пробных точках (в общем случае — во всех 2ⁿ или 2^n-p пробных точках). Проведение пробных опытов методом ПФЭ (или ДФЭ) позволяет также получать информацию о взаимодействиях факторов и достаточно просто осуществлять статистическую проверку результатов расчетов.

На первом цикле - метода крутого восхождения использу ется следующая процедура:

1. Выбирают основную (начальную, нулевую) точку К _о(рис. 6.4). Правила ее выбора прежние.

2. Выбирают интервал варьирования Dx_i для каждого фактора x_i (i= Т, 2,..., п). Правила выбора Dx_i изложены выше.

3. Определяют координаты пробных точек для нижнего и верх­него уровней варьирования факторов x_i по правилам ПФЭ (см/тему 3)

x_iн=x_i0-Dx_i, x_iв+Dx_i (6.18)

и составляют ортогональную матрицу планирования ПФЭ или ДФЭ, для чего факторы нормируют по формуле

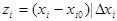. (6.19)

Затем выбирают число m серий параллельных опытов, порядок проведения опытов в сериях рандомизируют с помощью таблицы случайных чисел (см. Приложение I) и в этом порядке выполняют наблюдения отклика в точках ПФЭ и ДФЭ (на рис. 6.4 это К₁, К₂, К₃, К₄).

4. По результатам ПФЭ (или ДФЭ) вычисляют оценки коэффициентов нормированного уравнения регрессии первого порядка*

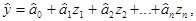(6.20)

* Для оценивания степени кривизны поверхности отклика могут вычисляться также коэффициенты при взаимодействиях z_iz_l. Расчетные формулы для получения 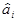и 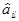даны в теме 3. В дальнейшем будем говорить о ПФЭ, подразумевая, что возможен и ДФЭ.

а также производят статистическую проверкузначимости 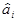, для чего можно рассчитать критическое значение коэффициентов:

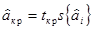, (6.21)

где t_зн=t_табл{n_зн;q}, выбираемое из таблицы (см. Приложение V) при числе степеней свободы n_зн=N(m-1) и принятом уровне значимости q.

5. Вычисляют расчетные i-e составляющие рабочих шагов в реальном масштабе:

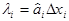. (6.22)

Максимальное по модулю из всех l_i (i= 1, 2,..., п) принимают за базовое l_баз.

6. Получают практические (округленные) i -е составляющие рабочих шагов 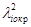для продвижения вдоль направления градиента (на рис. 6.4 это луч K_oA ), для чего округляют (иди изменяют) l_баз до удобного l_{баз.окр} и пропорционально этому округляют (или изменяют) остальные l_i до l_iокр(i=1, 2,..., п). Округление l_i производят по формуле

l_iокр=(l_{баз.окр}/l_баз)l_i (6.23)

до удобного значения либо с учетом погрешностей измерения по каждому фактору x_i. Знаки l_iокр должны соответствовать* знакам оценок 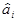коэффициентов.^:

7. Вычисляют координаты k-x рабочих точек (k=1, 2,...) на направлении градиента (на рис. 6.4 это точки К₅ — К₁₀) в реальном масштабе:

x_ik=x_i0+kl_iокр; (6.24)

в них последовательно выполняют мысленные и проверочные (реальные) опыты. Размер l_i обычно выбирают так, чтобы первая рабочая точка (k = 1) не выходила за границы области ПФЭ.

Мысленные опыты заключаются в получении предсказанных (расчетных) значений отклика 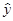по полученному линейному уравнению (6.20). Они позволяют: 1) сокращать объем реальных опытов, т. е. увеличивать скорость продвижения к экстремуму; 2) иметь представление, насколько хорошо уравнение (6.20) аппроксимирует реальную поверхность отклика (рис. 6.5), т. е. насколько расчетные значения 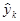отличаются от результатов наблюдавшихся значений y_kнабл в реальных опытах; 3) оценивать правильность выбора размера составляющих практического рабочего шага (l_iокр): если за число шагов k=3 достигается и превышается максимально возможное расчетное значение целевой

· Если отыскивается минимум, то знаки l_iокр должны быть противоположны знакам .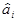

функции (определяемое из физических свойств и ограничении, существующих для объекта), то l_iокр нужно уменьшить; если же число k слишком большое, то l_iокр следует увеличить либо реже ставить реальные опыты.

Реальные (проверочные) опыты в начале движения из базовой точки вдоль направления градиента ставят через 2 — 4 мысленных опыта, а при уменьшении приращений наблюдавшихся значений отклика у_набл в каждом последующем реализованном опыте по сравнению с предыдущим в рабочих точках проверочные опыты ставят чаще, вблизи же частного экстремума выполняют на каждом шаге. Рабочее движение продолжают, пока не будет достигнут частный экстремум на направлении градиента (на рис. 6.4 это точка К₈). Признаком достижения частного экстремума является уменьшение отклика в последующих проверочных опытах.

8. Точку частного экстремума на первоначальном направлении градиента (на рис. 6.4 это точка К₈ на луче К₀А) принимают за новую нулевую точку и организуют второй цикл крутого восхождения. Порядок работы на втором цикле тот же, что и на первом. Различие состоит в том, что интервалы варьирования при постановке пробных опытов (ПФЭ) и размер, рабочих шагов в связи с приближением к экстремуму и увеличением кривизны поверхности отклика обычно выбирают меньшими, чем на первом цикле. В случае необходимости выполняют третий цикл крутого восхождения.

9. Поисковое рабочее движение прекращают по достижении области экстремума. Признаком достижения экстремума является статистическая незначимость оценок 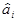коэффициентов при членах первого порядка, вычисленных по результатам ПФЭ (ДФЭ) вокруг очередной нулевой точки.

Достоинства метода крутого восхождения: 1) высокая помехозащищенность (помехоустойчивость) в смысле точности оценивания составляющих градиента: если в градиентных методах каждая составляющая 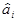оценивается лишь по двум точкам факторного пространства, то в ПФЭ, который в методе крутого восхождения используется для этой цели, каждый коэффициент, оценивается по всем N = 2ⁿ точкам; 2) высокая эффективность в смысле скорости движения к экстремуму; по сравнению с методом Гаусса—Зайделя она выше за счет продвижения по градиенту, а по сравнению с градиентными—за счет исключения пробных опытов на каждом рабочем шаге и за счет мысленных опытов; 3) пробные опыты, выполняемые методом ПФЭ, позволяют получать информацию об оценках 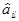коэффициентов при взаимодействиях факторов z_i z_l, характеризующих кривизну поверхности отклика; увеличение 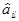при уменьшении 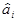обычно характеризует приближение к экстремуму; 4) ПФЭ с применением параллельных опытов позволяет достаточно просто осуществлять надежную статистическую интерпретацию результатов; 5) метод наиболее эффективен из всех известных при пологих поверхностях отклика.

Недостатком рассмотренного метода является несколько большая, чем в предыдущих методах, сложность планирования пробных опытов, требующая одновременного варьирования сразу всех факторов относительно базовой точки, и меньшая оперативность по сравнению с симплексным методом (см. ниже) в условиях дрейфующих объектов.