2014-02-10
1460
Если правая часть дифференциального уравнения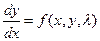 
(1) непрерывна по λ при 
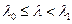и удовлетворяет условиям теоремы Пикара, причём постоянная Липшица не зависит от λ, то решение y = y(x, λ) (2) уравнения (1), удовлетворяющего условию 
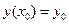непрерывно зависит от λ.
Доказательство.
Аналогично доказательству теоремы Пикара.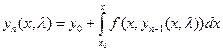 
(3), при .
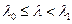Тем же методом можно показать непрерывную зависимость решения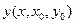 
уравнения 
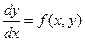от начальных значений 
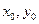. При этом только уменьшается h
Вопрос о непрерывной зависимости решения от начальных данных сводится к вопросу о непрерывной зависимости решения от параметра. Сделаем замену: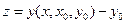 
(4), 
.
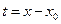Тогда уравнение 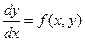,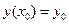переходит в уравнение 
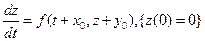(5), к которому уже можно применить теорему о непрерывной зависимости решения от параметров 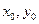(f удовлетворяет условиям теоремы Пикара).
Непрерывная зависимость от начальных данных, т.е. 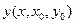, где 
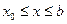(или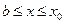 
) означает, что для 
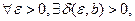что из неравенств 
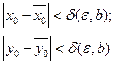следует, что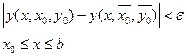 
С возрастанием b число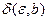 
, как правило, уменьшается.
Особый интерес вызывает решение, которое мало изменяется при произвольном, но малом изменении начальных значений для сколь угодно больших значений аргумента. Такое решение называется устойчивым.
|
|
|
