Решение. Задача о кратчайшем пути

Задача о кратчайшем пути

Матричный способ задания сетей

Матричное представление структуры сети дает более удобный способ описания, чем графическое, особенно при большом числе вершин и дуг. Взаимосвязь между вершинами сети можно определить при помощи матрицы смежности вершин графа. Это квадратная матрица n -го порядка, строки и столбцы которой соответствуют вершинам графа. Элементы 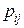матрицы равны 1, если существует дуга (i, j) и 0 – в противном случае. Например,матрицы смежности вершин графа, изображенного на рис. 6. 1 имеет вид

№ вершины

Для неориентированной сети матрица является симметричной. Количественные характеристики дуг сети. а также взаимосвязь между ее вершинами могут быть представлены с помощью матрицы весовых коэффициентов, которая задается массивом 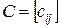(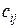– количественный параметр, обычно называемый длиной дуги (i, j), 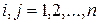). Для неориентированной сети матрица является симметричной.

Одной из наиболее важных оптимизационных задач на сети является задача нахождения цепи, соединяющей два узла – исходный узел S и узел назначения Т, которая имеет минимальную возможную длину. Алгоритм нахождения кратчайшего пути для сетей без циклов предложен Дейкстрой в 1959г. и считается одним из наиболее эффективных. Он основан на приписывании узлам либо временных, либо постоянных пометок и имеет рекурсивный характер. Все вычисления выполняются с использованием информации об уже определенных на предшествующих шагах кратчайших расстояниях.

Для заданного узла j через 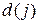обозначим оценку длины кратчайшей цепи из исходного узла S в этот узел. Если эта оценка не может быть улучшена, то она называется «постоянной пометкой» и обозначается 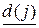. В противном случае она называется «временной пометкой». Обозначим через y номер вершины, получившей постоянную пометку последней. Алгоритм состоит из трех шагов.

Шаг 1. Всем узлам, кроме исходного, приписываются временные пометки, равные 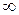, т.е. 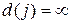. Исходному узлу приписывается постоянная пометка, равная нулю, т.е. 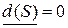и .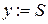

Шаг 2. Рассматриваем все вершины j, смежные с последней получившей постоянную пометку вершиной и имеющие временные пометки. Сравниваем величину временной пометки 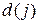с суммой величины последней постоянной пометки 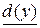и длины дуги 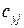, ведущей из y в рассматриваемую вершину. Временной пометке рассматриваемого узла присваиваем минимальное значение из двух сравниваемых величин:

.

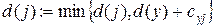Среди всех временных пометок выбираем минимальную (пусть это пометка вершины 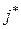) и делаем ее постоянной, т.е. 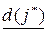и 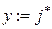. Кроме того, помечаем дугу 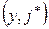, ведущую в выбранную на данном этапе вершину. Если все временные пометки равны бесконечности, т.е. 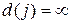, то в исходном графе отсутствует путь из S в эти вершины и вычисления заканчиваются.
Шаг 3. Если последняя постоянная пометка приписана узлу Т 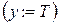, то алгоритм завершает работу: кратчайший путь из вершины S в узел назначения Т найден. Иначе повторяем шаг 2.

В процессе решения помеченные дуги образуют в исходном графе ориентированное дерево кратчайших путей с корнем в вершине S – т.е. путь от вершины S до любой вершины, принадлежащей дереву, – кратчайший. Кроме этого, если вершина y принадлежит кратчайшему пути из S в j, то часть этого пути, заключенная между у и j, является кратчайшим путем из вершины у в j.

Алгоритм Дейкстры может быть выполнен непосредственно на сети.

Пример. Сеть дорог с двухсторонним движением задана матрицей расстояний в км (матрицей весовых коэффициентов). Необходимо найти для данной сети дорог самый короткий маршрут из пункта 1 в пункт 10.

Узлы

Схематически сетевая модель задачи изображена на рис. 6.3 в виде неориентированной сети.

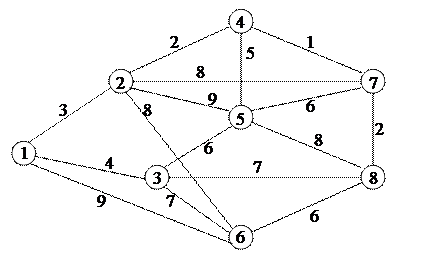
Рис. 6.3 Сетевая модель задачи.

Продемонстрируем работу алгоритма Дейкстры, отмечая временные и постоянные пометки непосредственно в узлах сети. Для этого каждый узел изобразим в виде овала и разделим его на три части следующим образом

Шаг 1. Исходному узлу приписываем постоянную пометку, равную нулю, т.е. 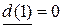и 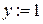. Всем остальным узлам, приписываем временные пометки, равные 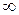, т.е. 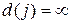, j = 2,…, 8. Отметим это на сети:

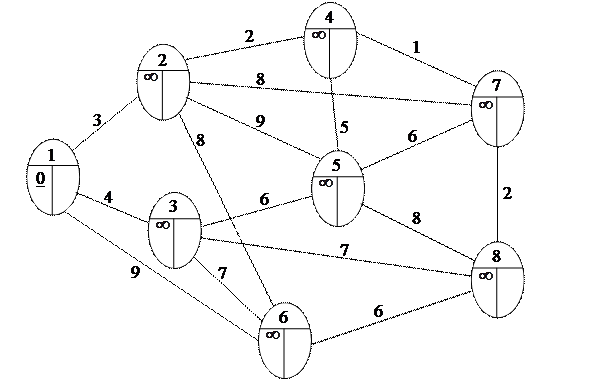
Шаг 2. Узлы 2, 3 и 6 смежные с последним, получившим постоянную пометку узлом 1. Новые значения временных пометок этих узлов будут:

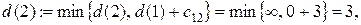
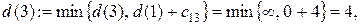
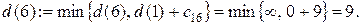
Минимальной временной пометкой является пометка узла 2, т.к. 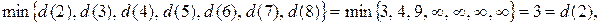поэтому она становится постоянной. Подчеркиваем ее и 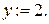Помечаем дугу 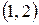. Отметим это на сети:

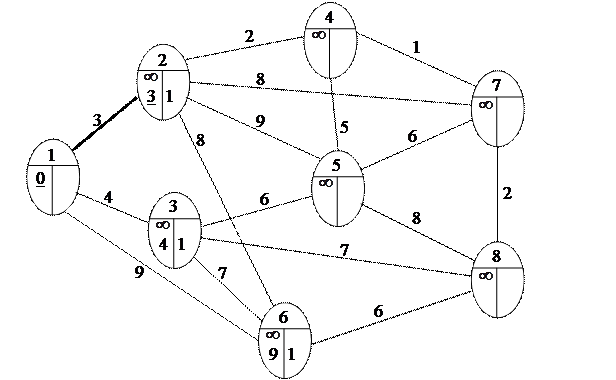
Шаг 3. Поскольку узел 8 не помечен постоянной пометкой, переходим к шагу 2.

Шаг 2. Узлы 4, 5, 6 и 7 смежные с последним, получившим постоянную пометку узлом 2. Новые значения временных пометок этих узлов будут:

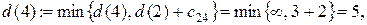
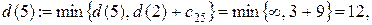
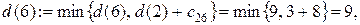
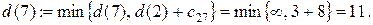
Минимальной временной пометкой является пометка узла 3, т.к. 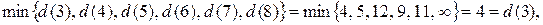поэтому она становится постоянной. Подчеркиваем ее и 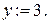Помечаем дугу 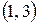. Отметим это на сети:

Шаг 3. Поскольку узел 8 не помечен постоянной пометкой, переходим к шагу 2.

Шаг 2. Узлы 5, 6 и 8 смежные с последним, получившим постоянную пометку узлом 3. Новые значения временных пометок этих узлов будут:

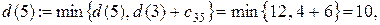
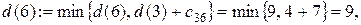
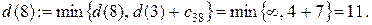
Минимальной временной пометкой является пометка узла 4, т.к. 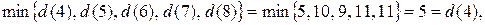поэтому она становится постоянной. Подчеркиваем ее и 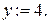Помечаем дугу 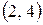. Отметим это на сети:

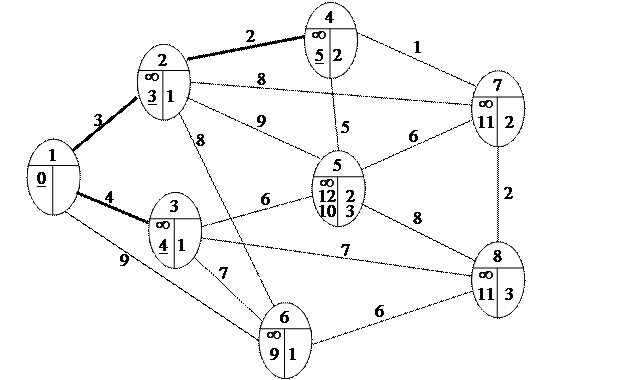
Шаг 3. Поскольку узел 8 не помечен постоянной пометкой, переходим к шагу 2.

Шаг 2. Узлы 5 и 7 смежные с последним, получившим постоянную пометку узлом 4. Новые значения временных пометок этих узлов будут:

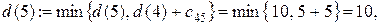
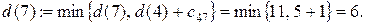
Минимальной временной пометкой является пометка узла 7, т.к. 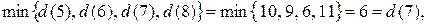она становится постоянной. Подчеркиваем ее и 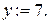Помечаем дугу 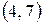. Отметим это на сети:

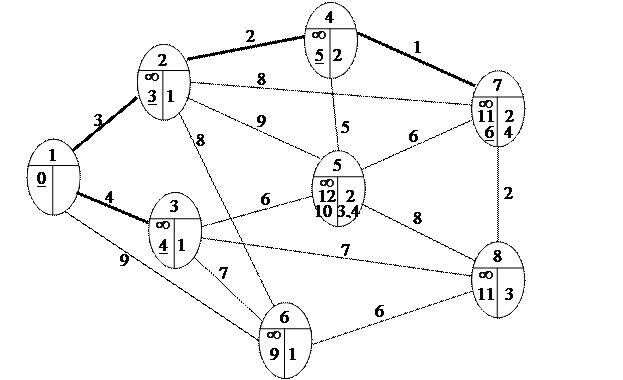
Шаг 3. Поскольку узел 8 не помечен постоянной пометкой, переходим к шагу 2.

Шаг 2. Узлы 5 и 8 смежные с последним, получившим постоянную пометку узлом 7. Новые значения временных пометок этих узлов будут:

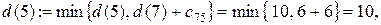
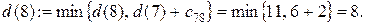
Минимальной временной пометкой является пометка узла 8, т.к. 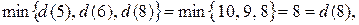она становится постоянной. Подчеркиваем ее и 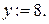Помечаем дугу 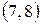. Отметим это на сети:

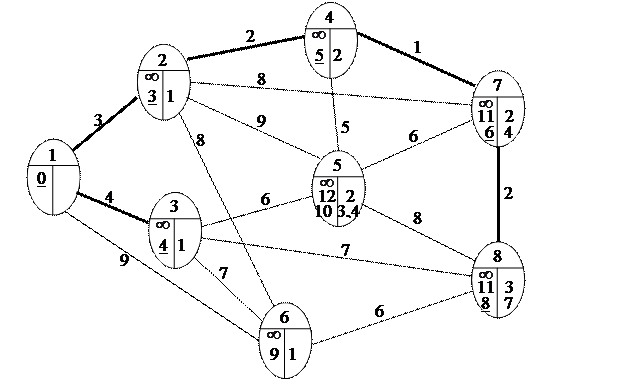
Шаг 3. Поскольку узел 8 помечен постоянной пометкой, то алгоритм завершает работу: кратчайший путь из узла 1 в узел назначения 8 найден.

Построенное дерево кратчайших путей состоит из дуг (1, 2), (1, 3), (2, 4), (4, 7), (7, 8) (они помечены на последней сети). Кратчайший путь от узла 1 до узла 8 составляет 8 км, т.к. постоянная пометка этого узла 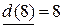и состоит из дуг (1, 2), (2, 4), (4, 7), (7, 8).