Определение. Будем говорить, что в векторном пространстве Rnвведена операция скалярного умножения векторов (или просто скалярное умножение), если любой паре векторов a и b из Rnпоставлено в соответствие действительное число, обозначаемое a × b (или ( a, b )) и называемое скалярным произведением векторов a и b, и это соответствие для любых векторов a, b, и c и любого действительного числа k удовлетворяет условиям:
1°. a × b = b × a;
2°. a ×(b + c) = a × b + a × c;
3°. (k a)× b = k( a × b );
4°. a × a ³ 0, при этом равенство справедливо в том и только том случае, когда a = 0.
Условия 1°–4° называются аксиомами скалярного умножения.
Следствия из аксиом:
1. (a + b)× c = a × c + b × c;
2. a ×(k b) = k (a × b);
3. a × 0 = 0.
Следствие 1 получим из цепочки равенств:
(a + b)× c = c × (a + b) = c × a + c × b = a × c + b × c.
Аналогично доказывается следствие 2.
Докажем следствие 3:
a × 0 = a ×(0× a) =0× (a, a)=0.
Определение. Векторное пространство, в котором введена операция скалярного умножения векторов, называется евклидовым пространством.
|
|
|
Скалярное произведение двух векторов 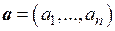 и
и 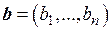 можно определить равенством
можно определить равенством
 . (1.9)
. (1.9)
Справедливость аксиомы 1° для определенного формулой (1.9) скалярного произведения очевидна. Проверим справедливость аксиом 2° и 3°.
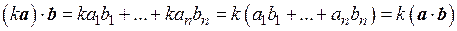 ;
;

Справедливость аксиомы 4° вытекает из того, что 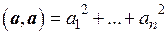 всегда является неотрицательным действительным числом и обращается в ноль лишь при условии
всегда является неотрицательным действительным числом и обращается в ноль лишь при условии 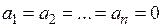 .
.
После того, как в векторном пространстве Rnвведено скалярное произведение, можно определить такие понятия, как модуль (длина) вектора, угол между векторами, ортогональность векторов.
Определение. Длиной вектора a называют число | a |=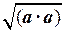 .
.
Такое определение длины вектора имеет смысл, т.к. это число неотрицательно (в силу аксиомы 4°) и нулевой вектор имеет нулевую длину.
Определение. Пусть a и b – два ненулевых вектора. Углом между ними называют число j, определенное с помощью равенства
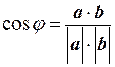 (1.10)
(1.10)
и удовлетворяющее условию 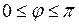 .
.
Не всякое число можно принять за косинус угла: равенство 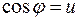 возможно только при условии
возможно только при условии 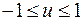 . Следовательно, угол j между ненулевыми векторами a и b существует только в том случае, когда
. Следовательно, угол j между ненулевыми векторами a и b существует только в том случае, когда

или, что то же самое,
 . (1.11)
. (1.11)
Теорема 1.4. Для любых векторов a и b в евклидовом пространстве Rn справедливо неравенство
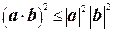 . (1.12)
. (1.12)
Неравенство (1.12) называют неравенством Коши–Буняковского.
□ Пусть c = b – t× a где t – произвольное действительное число.
Рассмотрим скалярный квадрат вектора c:
(b – t× a, b – t× a)= (b, b) – t (a, b) – t (b, a) + t2(a, a).
Мы получили равенство вида
(b – t× a, b – t× a)= a t2 –2b t + g, где a= (a, a), b= (a, b), g= (b, b).
Квадратный трехчлен относительно t в правой части этого равенства при любом значении t неотрицателен, поскольку равен скалярному квадрату вектора c. Следовательно, дискриминант b2– ag уравнения
|
|
|
at2–2bt+g=0 (a≠0)
не может быть положительным, т.е.
(a, b)2– (a, a) (b, b) £ 0, (1.13)
что является лишь другой записью неравенства (1.12).
В случае a=(a, a)=0 квадратный трехчлен вырождается в линейную функцию, но в этом случае вектор a является нулевым, так что (a, b)=0 и неравенство (1.13) также справедливо. ■
Равенство c = 0 означает, что b – t× a = 0, или b = t× a, то есть вектор b коллинеарен вектору a. В этом случае из формулы (1.10) следует, что угол между векторами a и b равен нулю или p.
Итак, доказано неравенство Коши–Буняковского и тем самым обоснована правомерность данного определения угла между векторами.
Из равенства (1.10) следует, что скалярное произведение векторов можно определить следующим образом:
 (a, b) = | a |×| b |×cos j, (1.14)
(a, b) = | a |×| b |×cos j, (1.14)
т.е. скалярное произведение двух векторов равно произведению длин этих векторов на косинус угла между ними.
Пример. Пусть скалярное произведение векторов задается
формулой (1.9)
 , или
, или 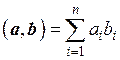 .
.
Тогда  ,
, 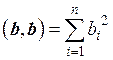 .
.
Неравенство Коши-Буняковского можно записать в виде:
 .
.
Следствие неравенства Коши-Буняковского. Для любых векторов a и b в евклидовом пространстве R2 имеет место неравенство
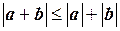 .
.
□ В силу аксиом скалярного произведения имеем
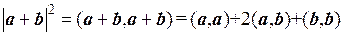 .
.
Так как (в силу неравенства Коши-Буняковского) 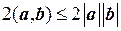 , то
, то
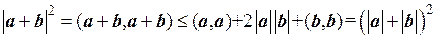 ,
,
т.е. 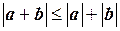 , что и требовалось доказать. ■
, что и требовалось доказать. ■
 2014-02-12
2014-02-12 3679
3679







